Stars and Planets

—Birth—
Chris Ormel

Roadmap module 4
Initial Mass Function (IMF)
The initial distribution of stars (after their formation) by their mass
Eddington Luminosity
The Luminosity at which radiation outweighs gravity
Virial Theorem
A fundamental relation between kinetic/thermal energy and gravitational energy for "relaxed" systems of many particles (stars as well as gas). Frequently employed by astronomers to find the "dynamical mass".
Jeans Mass
a critical mass above which the cloud will collapse
Dispersion relationship
A relation how a fluid responds to perturbations on a certain scale. A frequently used tool to investigate whether fluids are stable
Protoplanetary Disks
The environment where planets are born
Disk instability and core accretion
Planet formation models that describe the formation of terrestrial planets, the cores of giant planets, and gas giants
- Toomre Q criterion
- Giant planet formation
- planetesimal formation
- Coagulation
- Gravitational focusing
- Pebble accretion
Topics
- Virial theorem
- Cloud collapse/SF
- Eddington luminosity
- Dispersion analysis
- Elements of planet formation
Virial theorem
— read CO 2.4 —
- The
Virial Theorem
postulates that
for self-gravitating systems:
-
![]() for an N-particle system;
for an N-particle system;
-
![]() for gaseous objects
for gaseous objects
where nvir is a positive number, T is the kinetic, Uint the internal energy and W the total gravitational (potential) energy and <..> denotes the time-average. In other words, the virial theorem holds when the system has relaxed into a steady configuration.
Proof goes along these lines. The quantity
![]()
time-averages to 0. Q (the "virial") is itself the derivative of the moment of inertia. For a gravitating gas, we derive from the hydrostatic balance equation
![]()
To proceed,
![]() must be linked to the internal energy per unit mass
must be linked to the internal energy per unit mass
![]() . For an ideal gas this is just
. For an ideal gas this is just
![]()
where
![]() is the number of free degrees and
is the number of free degrees and
![]() is the heat capacity ratio. For a mono-atomic gas,
is the heat capacity ratio. For a mono-atomic gas,
![]() ,
,
![]() and
and
![]() .
.
-

Virial theorem
— read CO 2.4 —
- The
Virial Theorem
postulates that
for self-gravitating systems:
-
![]() for an N-particle system;
for an N-particle system;
-
![]() for gaseous objects
for gaseous objects
where nvir is a positive number, T is the kinetic, Uint the internal energy and W the total gravitational (potential) energy and <..> denotes the time-average. In other words, the virial theorem holds when the system has relaxed into a steady configuration.
-
- Specific examples include:
-
![]() (fully ionized or mono-atomic gas)
(fully ionized or mono-atomic gas)
-
![]() (radiation gas)
(radiation gas)
-

Virial theorem
— read CO 2.4 —
- The
Virial Theorem
postulates that
-
![]() for an N-particle system;
for an N-particle system;
-
![]() (fully ionized or mono-atomic gas)
(fully ionized or mono-atomic gas)
-
![]() (radiation gas)
(radiation gas)
-
- The virial theorem is not the same as energy conservation!
Conservation of energy dictates that
![]() where the total energy E is conserved in an isolated system. Hence we obtain that objects in virial equilibrium have
where the total energy E is conserved in an isolated system. Hence we obtain that objects in virial equilibrium have
![]() (a different prefactors may apply if the gas is not mono-atomic).
(a different prefactors may apply if the gas is not mono-atomic).
Note — the expression for the virial theorem can be extended to include magnetic support, rotational support etc..

Virial theorem
— read CO 2.4 —
- The
Virial Theorem
postulates that
-
![]() (fully ionized or mono-atomic gas)
(fully ionized or mono-atomic gas)
-
![]() (radiation gas)
(radiation gas)
-
- The virial theorem is not the same as energy conservation!
- Applications:
- (Proto-)stars heat up when they contract:
![]()
Protostars (no nuclear burning) lose energy. Of the gravitational energy liberated during contraction, half is radiated and the other half goes into internal energy. Stars heat up while loosing energy!
This corresponds to moving from state A → B in the figure right - Stars are thermodynamically stable
They expand and cool down when their total energy E increases (!). This corresponds to moving from B → A in the figure right. This kind of "virial stability" only applies to the ideal gas law.
- Obtain the (dynamical) mass by measuring the linewidth.
- (Proto-)stars heat up when they contract:

virial theorem — applications


Andromeda-Milky Way merger

The Andromeda galaxy will be merging with the Milky Way galaxy in a few billion years. Assume the galaxies are equal in their properties (mass, size, rotation velocity) and that the merger product is again a spiral galaxy.
By the virial theorem, what is the rotational velocity of the merger galaxy?
- lower than the present-day
- the same
- higher than the present-day
Also, what is the radius R of the merger galaxy?
- slightly smaller than the present size
- the same as the present size
- slightly larger than the present
- slightly smaller than 2x the present
- twice that of the present
- larger than 2x the present
Star formation
— read CO 12.2 —
The condition for a spherical, uniform cloud to collapse is when its mass exceeds the Jeans mass

When
 the total energy of the cloud decreases when it is perturbed. If we insert numerical constants for the numbers and write the densities in terms of the number density
the total energy of the cloud decreases when it is perturbed. If we insert numerical constants for the numbers and write the densities in terms of the number density
 we obtain
we obtain

Note some (giant) clouds have
 suggesting that the should collapse! In reality, these clouds feature additional support mechanisms (like magnetic support). Hence the condition
suggesting that the should collapse! In reality, these clouds feature additional support mechanisms (like magnetic support). Hence the condition
 is a necessary but not (always) sufficient condition for collapse.
is a necessary but not (always) sufficient condition for collapse.
Star formation
— read CO 12.2 —
If the cloud is out of equilibrium, it collapses on a free-fall time

- During collapse of the cloud, ρ increases and the Jeans mass decreases. The cloud fragments with the fragments collapsing on their own.
- The isothermal collapse, requires efficient cooling.
- An increase in temperature, on the other hand, opposes cloud fragmentation, causing MJeans to rise
Star formation
— read CO 12.2 —
- An increase in temperature, on the other hand, opposes cloud fragmentation, causing MJeans to rise
- By balancing the heat generated by the collapse
![]() with the expression
for blackbody radiation
with the expression
for blackbody radiation
![]() applicable when the cloud starts to cool less efficienty (T becomes adiabatic) we can solve for the mass where the fragmentation terminates
where I have omitted numerical factors and ε~0.1 is an efficiency factor. For T=103 K, we obtain
applicable when the cloud starts to cool less efficienty (T becomes adiabatic) we can solve for the mass where the fragmentation terminates
where I have omitted numerical factors and ε~0.1 is an efficiency factor. For T=103 K, we obtain![]()
![]() .
.
This is of course an extremely crude estimate. But it tells that the protostar that forms at the end of the collapse state are of stellar mass — not of planet mass or the mass of galaxy. Further accretion onto this protostar will of course occur.

Initial mass function (IMF)
— read CO p.430 —
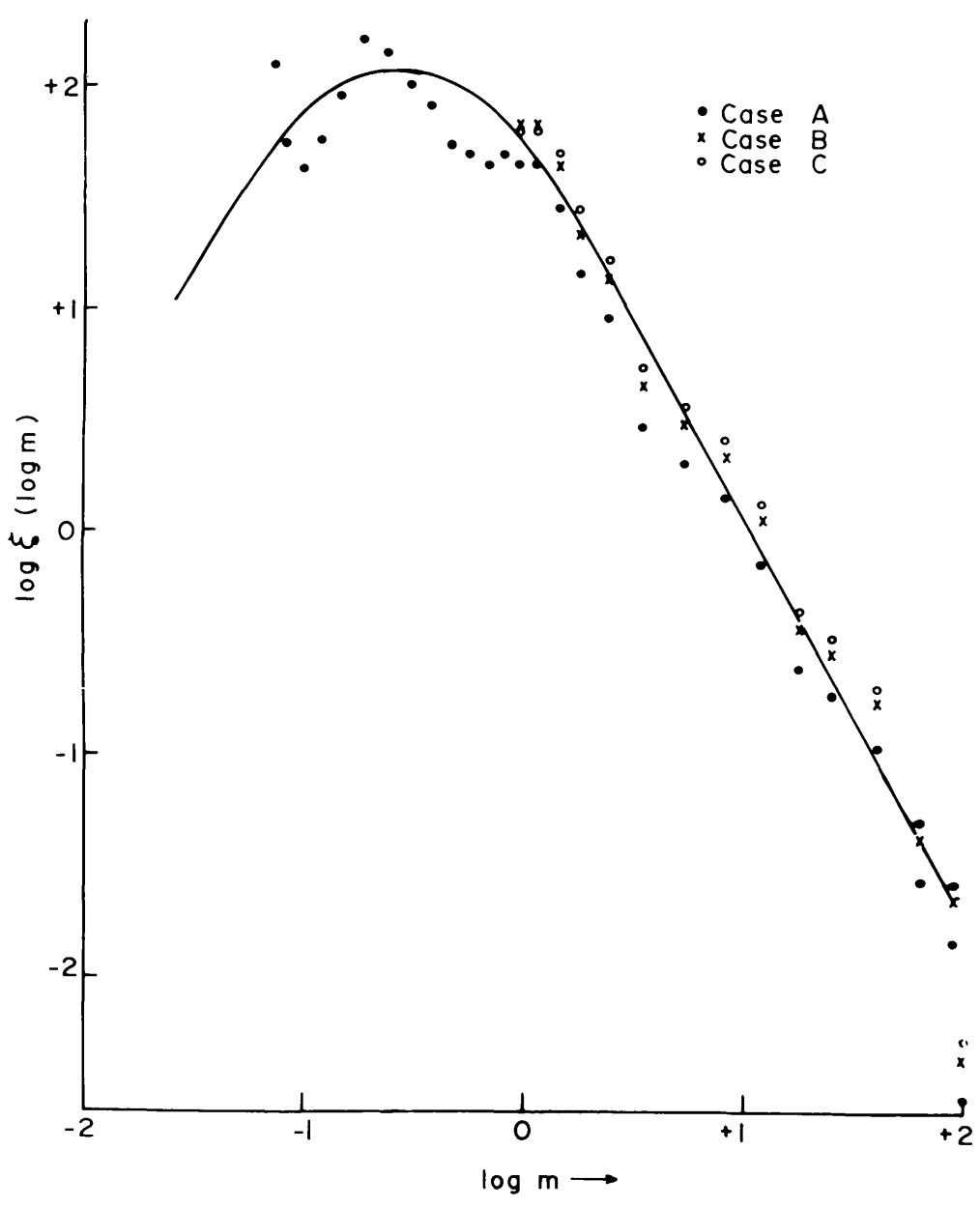
The Initial Mass Function or simply IMF is the distribution of stars formed by stellar mass

So ξ(m)Δm gives the number of stars that are formed in mass interval [m,m+Δm]
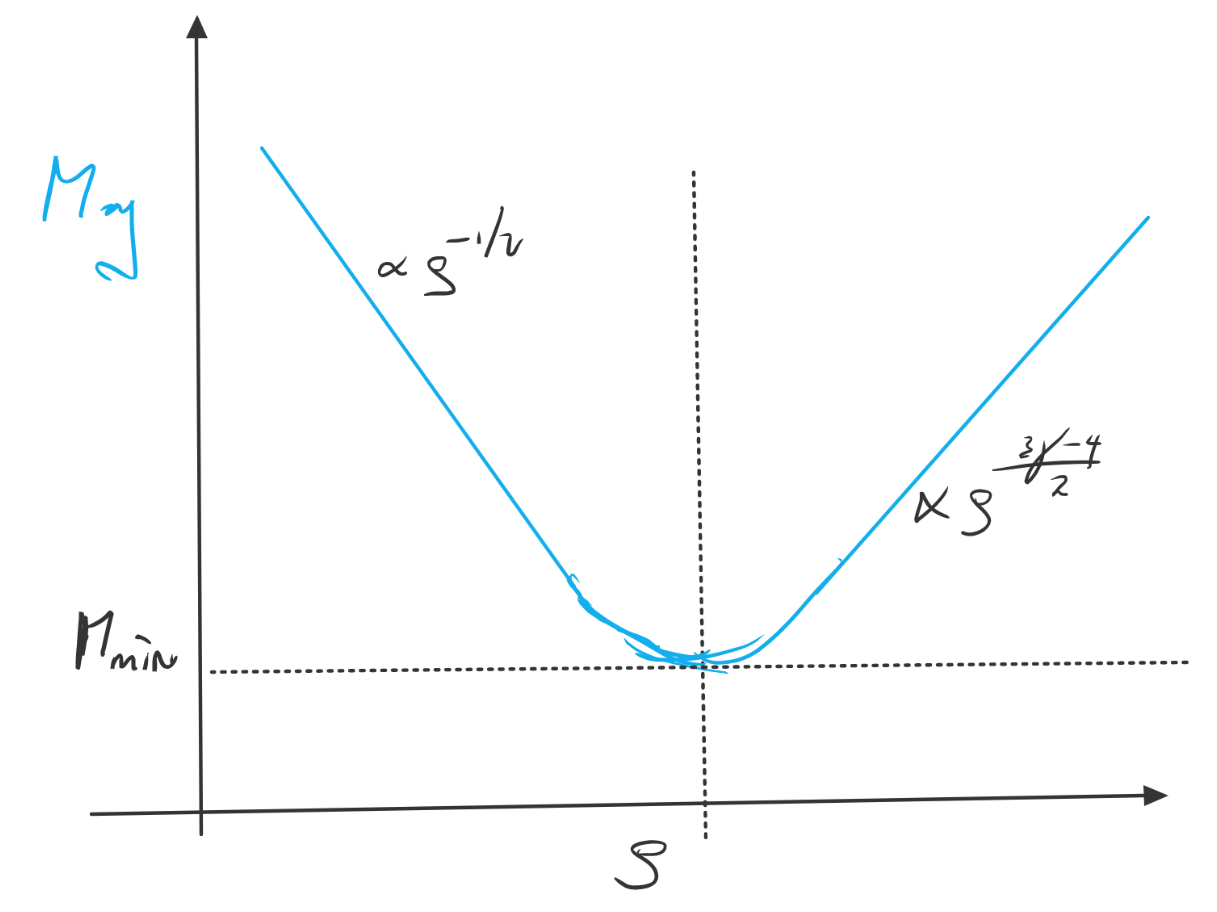
The IMF follows (steep) power-laws at high masses, but it turns over at low stellar masses (it has to!)
The origin of the IMF is an area of active research in star formation
Eddington Luminosity
— read CO 10.6 —
Accelerating charges radiate energy at a rate (Larmor formula):

(cgs units) with P is the power, q the charge
 the acceleration, c the speed of light.
the acceleration, c the speed of light.
The Thomson cross section for photons to interact with electrons

Valid in the low-energy (no recoil) limit,
 the photon energy does not change.
It follows from equating the radiated power to the incoming energy flux:
the photon energy does not change.
It follows from equating the radiated power to the incoming energy flux:

The Thomson cross section can also be obtained by equating the electrostatic energy corresponding to a sphere of radius rT with the rest energy of the electron
 The corresponding cross section
The corresponding cross section
 is the Thompson cross section barring numerical constant.
is the Thompson cross section barring numerical constant.
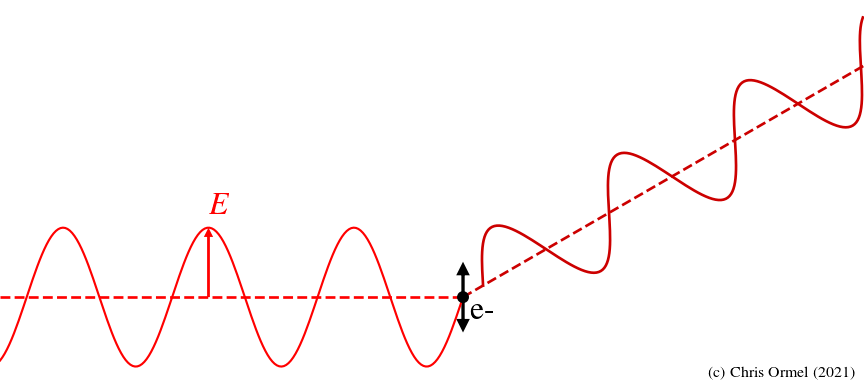
schematic of the interaction of an electromagnetic wave with a charged particle. Due to oscillating E-field, the particle (electron) experiences a force of

in the direction of the E-field, causing it to radiate. In the low-energy limit, the frequency of the radiation is just the same as that of the incoming wave, resulting in a scattering of the EM-wave (Thomson scattering).
Eddington Luminosity
— read CO 10.6 —
The Thomson cross section for photons to interact with electrons

Valid in the low-energy (no recoil) limit,
 the photon energy does not change.
the photon energy does not change.
This results in a radiation force of

on the electrons, which when balanced with the gravitational force (acting on all baryons).
Eddington Luminosity
— read CO 10.6 —
Balancing with the gravitational force, results in the Eddington Luminosity

Another, more general, way to write this is, is in terms of the opacity κ — the cross section per unit mass κ=σ/(me+mp) in this case. We then obtain
 .
.
- For luminosities, L>LEddington the star will be ripped apart
- On the main-sequence, the stellar mass-luminosity relationship is a power-law
![]()
The Eddington Luminosity sets an upper mass for stars!

Dispersion relation
The fluid equations:

where the E.o.S is chosen as isothermal (constant temperature), such that cs — the isothermal sound speeed — is constant.
To 0th order, for a uniform cloud, the solutions to these equations read simply:

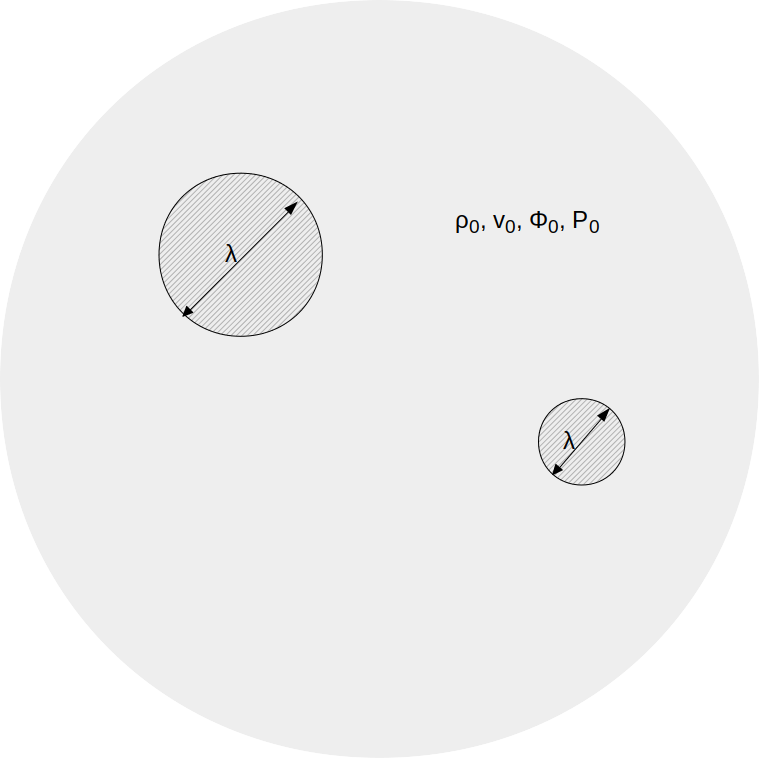
Dispersion relation
A linearly stability analysis quantifies how the system reacts to small perturbations that are wave-like in nature, e.g.,

with
 k the wavenumber and ω the frequency (or growth rate when it is imaginary!). Without loss of generality we have assumed that the wave travels in the x-direction. Note than ω can be complex, so the wave can grow (or decay)!
k the wavenumber and ω the frequency (or growth rate when it is imaginary!). Without loss of generality we have assumed that the wave travels in the x-direction. Note than ω can be complex, so the wave can grow (or decay)!
After some algebra, you arrive at the perturbation equations


Dispersion relation
The solution to the linearly stability analysis is the dispersion relationship:

A dispersion relationship is a relation between the scale of the perturbation (k) and the growth rate (ω).
We obtain:
- small scales (large k): ω2 is positive: perturbations remain wave-like and do not grow!
- large scales (small k): ω2 is negative: perturbations grow exponentially and are unstable!
- a critical scale
![]()
You can verify that
![]() amounts to the Jeans mass, barring a numerical coefficient
amounts to the Jeans mass, barring a numerical coefficient

Dispersion relation & planet formation
For disks the steady solution reads:

the assumption here is that the disk is thin. It does not need to be Keplerian rotating, but it should satisfy
 Also, we consider that the disk is axisymmetric (quantities do not depend on φ) and consider radial perturbations only (k oriented in the radial direction).
Also, we consider that the disk is axisymmetric (quantities do not depend on φ) and consider radial perturbations only (k oriented in the radial direction).
... and the dispersion relationship is

where
 is the epicycle frequency.
For a Keplerian potential
is the epicycle frequency.
For a Keplerian potential
 . Note that
. Note that
 has a minimum corresponding to the critical wavelength.
has a minimum corresponding to the critical wavelength.

Dispersion relation & planet formation
... and the dispersion relationship is

We obtain the following:
- The most critical wavelength is
![]()
- The disk becomes gravitationally unstable when the
Toomre-Q
parameter
![]()
- The corresponding mass is
![]() .
.
Question:
Is QT <1 the only criterion for gravitational instability to result in collapse?

Dispersion relation & planet formation
... and the dispersion relationship is

We obtain the following:
- The most critical wavelength is
![]()
- The disk becomes gravitationally unstable when the
Toomre-Q
parameter
![]()
- The corresponding mass is
![]() .
.
- In addition, gravitational collapse requires
fast enough cooling
Quantitatively,
![]() Otherwise the formed clumps will just be sheared apart
Otherwise the formed clumps will just be sheared apart

Dispersion relation & planet formation
... and the dispersion relationship is

We obtain the following:
- The most critical wavelength is
![]()
- The disk becomes gravitationally unstable when the Toomre-Q parameter QT<1.
- In addition, gravitational collapse requires
fast enough cooling
- For dust particles,
![]() can be used, amounting to a critical scale of
can be used, amounting to a critical scale of
![]()
Hence, particles need to settle. The settling of particles is promoted by the stellar gravity, but opposed by turbulence.
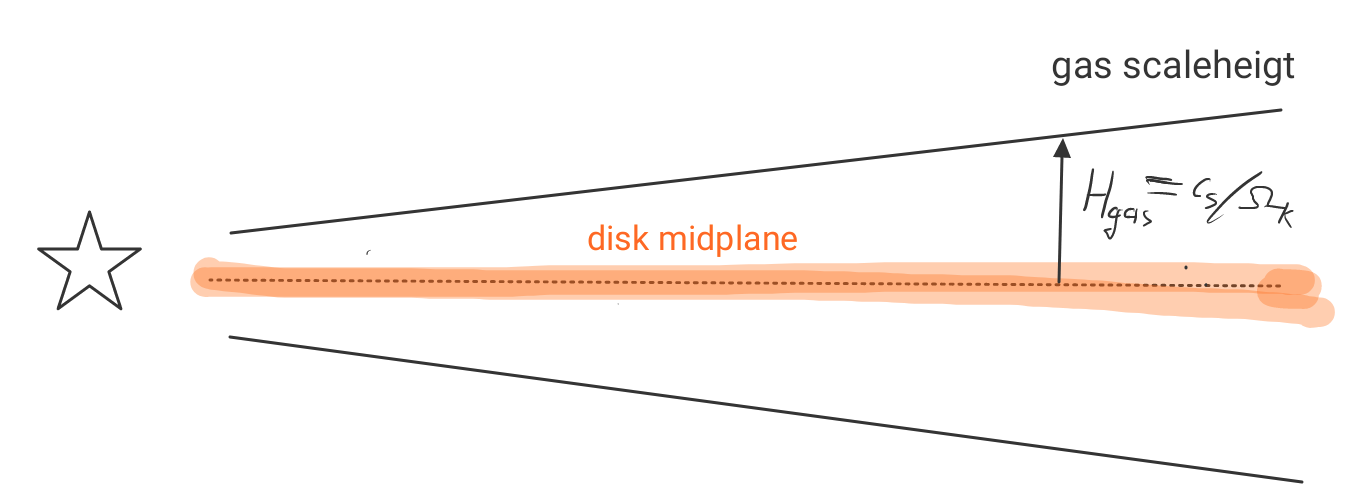
For the 2D analysis to remain valid, we must have
 (thin disks). In other words, particles must
settle
into a thin layer. This is the classical mechanism to form km-sized bodies (planetesimals), also known as the Goldreich-Ward mechanism, see Goldreich & Ward (1973)
(thin disks). In other words, particles must
settle
into a thin layer. This is the classical mechanism to form km-sized bodies (planetesimals), also known as the Goldreich-Ward mechanism, see Goldreich & Ward (1973)
effects of cooling
Smooth Particle Hydrodynamics (SPH) Simulations of gravitational instability in disks
- standard (fast cooling)
- slow cooling
effects of cooling
Smooth Particle Hydrodynamics (SPH) Simulations of gravitational instability in disks
- standard (fast cooling)
- slow cooling
Protoplanetary disks
What are we looking at?
This is hl tau, observed at mm-wavelengths by ALMA. These wavelengths trace the large dust particles in the disk midplane. Intriguing axisymmetric structure —rings— appear
figure credit wikipedia/ESO
you are looking here at mm-wavelength emission
these wavelengths trace the disk midplane
figure credit: DSHARP survey, ALMA, ESO, NAOJ, NRAO, S. Andrews , Nicolas Lira; original data: DSHARP.
Star formation — Classes
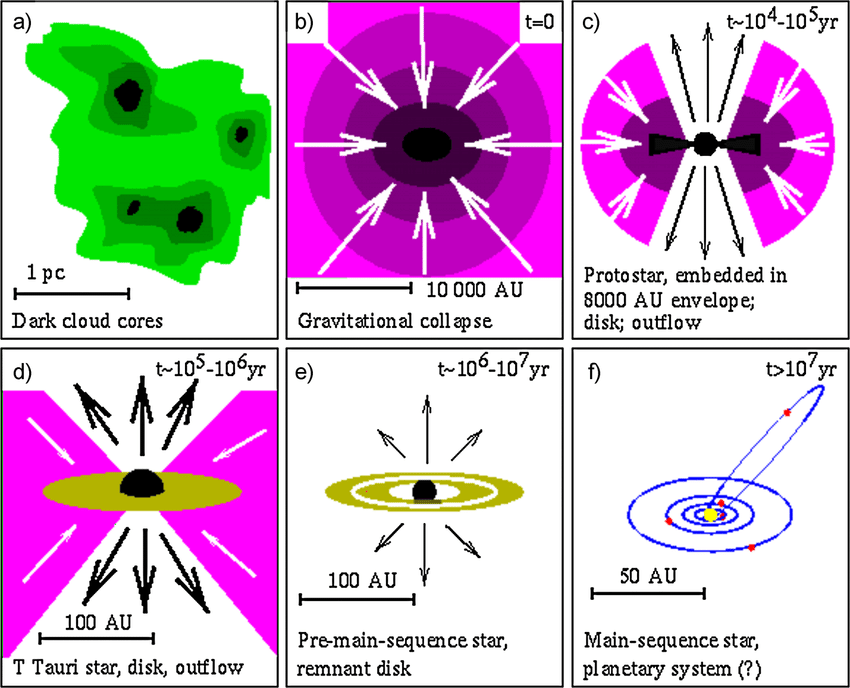
- Dark cores form and become unstable when their gravitational potential energy dominates thermal energy:
(mass exceeds Jeans mass)
![]()
- The collapse takes place on the free-fall timescale
this is the embedded phase Class 0
![]()
Star formation — Classes

- A star has formed. Class 1. An outflow develops, while material is still accreting onto the star. A disks forms.
- Accretion and outflow weaken. This is the stage where planets are thought to form. Class 2 or the T-Tauri phase.
- After the gas clears, a
debris disks
may be left
Debris disk consist of solid material that did not assemble into planetary bodies. In the solar system the asteroid belt and the Kuiper belt are debris disks
- A planetary system emerges. The final architecture of the planet system is set when orbital stability is reached.
the protoplanetary disks (observations)
read CO p.437—441 & Ch.23.2
Properties
- disks are naturally formed as byproduct of star formation due to angular momentum conservation
- disks are usually dusty, obscuring the interior disk midplane regions

the protoplanetary disks (observations)
read CO p.437—441 & Ch.23.2
Properties
- disks are naturally formed as byproduct of star formation due to angular momentum conservation
- disks are usually dusty, obscuring the interior disk midplane regions
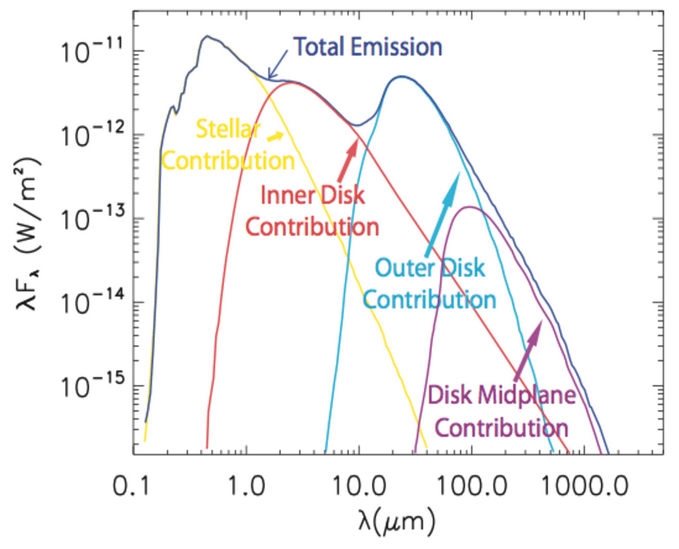
- the dust results in an
IR-excess
the total integrated emission is a superposition of several black body curves. The IR-excess is how disks were historically detected
the protoplanetary disks (observations)
read CO p.437—441 & Ch.23.2
Properties
- disks are naturally formed as byproduct of star formation due to angular momentum conservation
- disks are usually dusty, obscuring the interior disk midplane regions
- the dust results in an IR-excess

the protoplanetary disks (observations)
read CO p.437—441 & Ch.23.2
Properties
- disks are naturally formed as byproduct of star formation due to angular momentum conservation
- disks are usually dusty, obscuring the interior disk midplane regions
- the dust results in an IR-excess
-
Minimum-mass solar nebula (MMSN)
By spreading out the heavy element mass of the planets over rings, Weidenschilling (and Hayashi) obtained a crude prescription of the dust and gas density during the time of the formation of the planets. This prescription — known as the Minimum-Mass Solar Nebula — has many flaws, but serves as a useful benchmark. A frequently-used profile is:
![]()
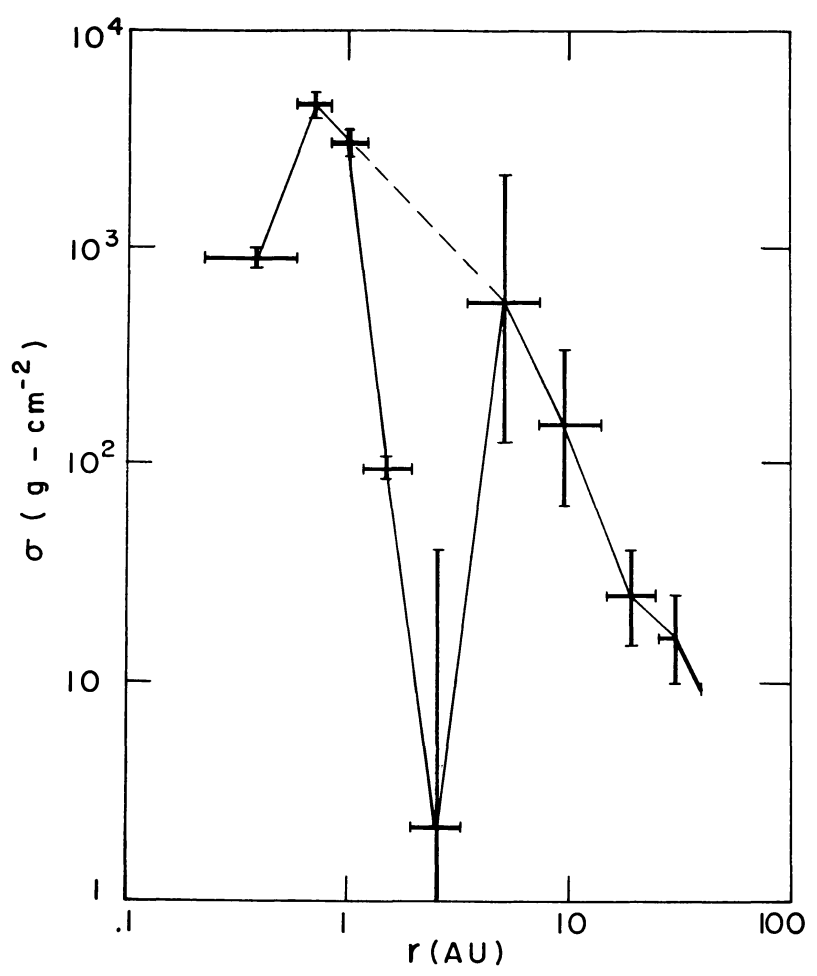
these numbers?
enough to fit a power-law!
the protoplanetary disks (observations)
read CO p.437—441 & Ch.23.2
Properties
- disks are naturally formed as byproduct of star formation due to angular momentum conservation
- disks are usually dusty, obscuring the interior disk midplane regions
- the dust results in an IR-excess
- Minimum-mass solar nebula (MMSN)
- disks are observed to
accrete
onto their host star at rates of
![]()
Mass and angular momentum are being transported.

The emission lines can be modeled, which provides the accretion luminosity Lacc. The accretion luminosity and accretion rate are related through:

the protoplanetary disks (observations)
read CO p.437—441 & Ch.23.2
Properties
- disks are naturally formed as byproduct of star formation due to angular momentum conservation
- disks are usually dusty, obscuring the interior disk midplane regions
- the dust results in an IR-excess
- Minimum-mass solar nebula (MMSN)
- disks are observed to
accrete
onto their host star at rates of
![]()
Mass and angular momentum are being transported.
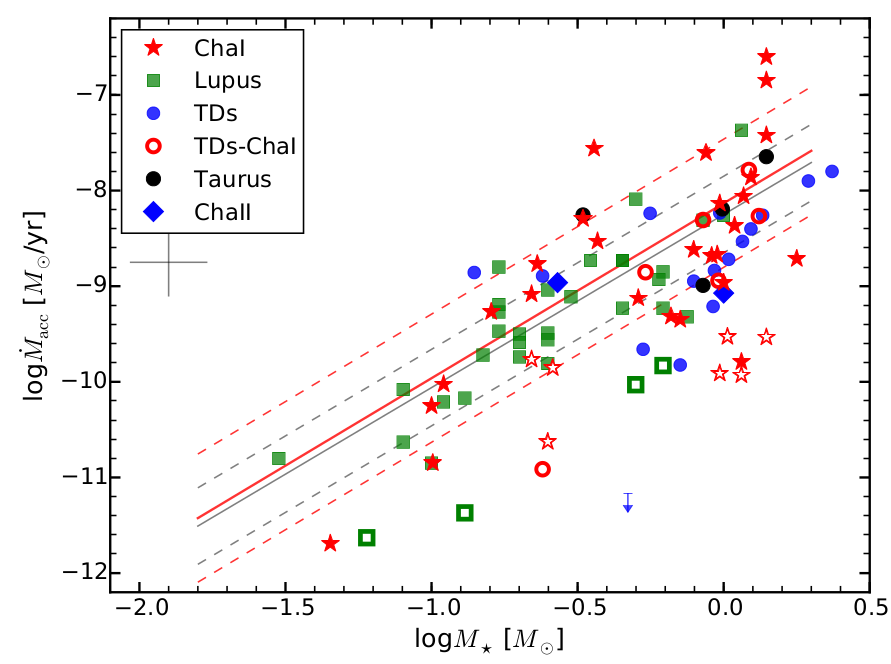
the protoplanetary disks (observations)
read CO p.437—441 & Ch.23.2
Properties
- disks are naturally formed as byproduct of star formation due to angular momentum conservation
- disks are usually dusty, obscuring the interior disk midplane regions
- the dust results in an IR-excess
- Minimum-mass solar nebula (MMSN)
- disks are observed to
accrete
onto their host star at rates of
![]()
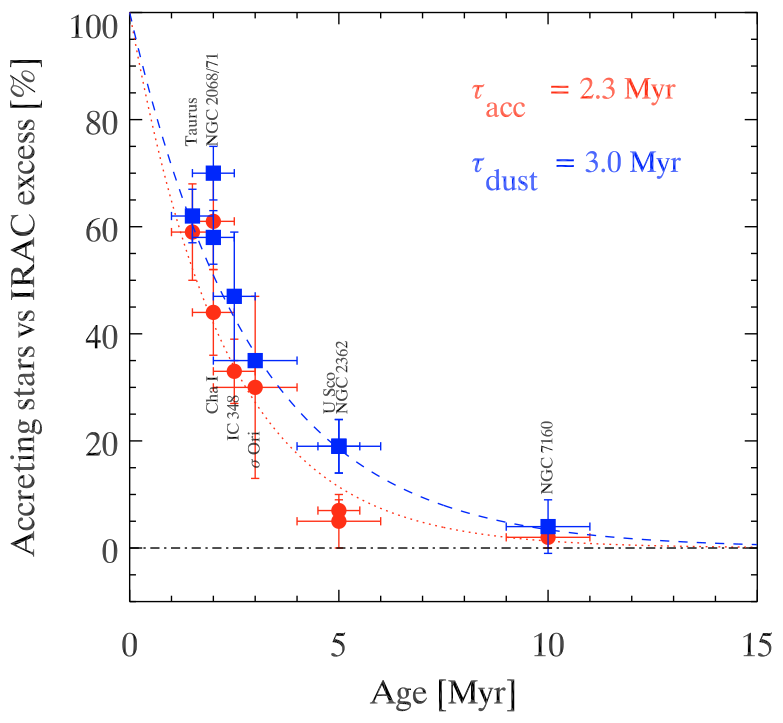
- Accretion terminates over timescales of ~Myr
A natural explanation is that the gas disk is gone after several Myr. It sets a timescale for the formation of gas giant planets
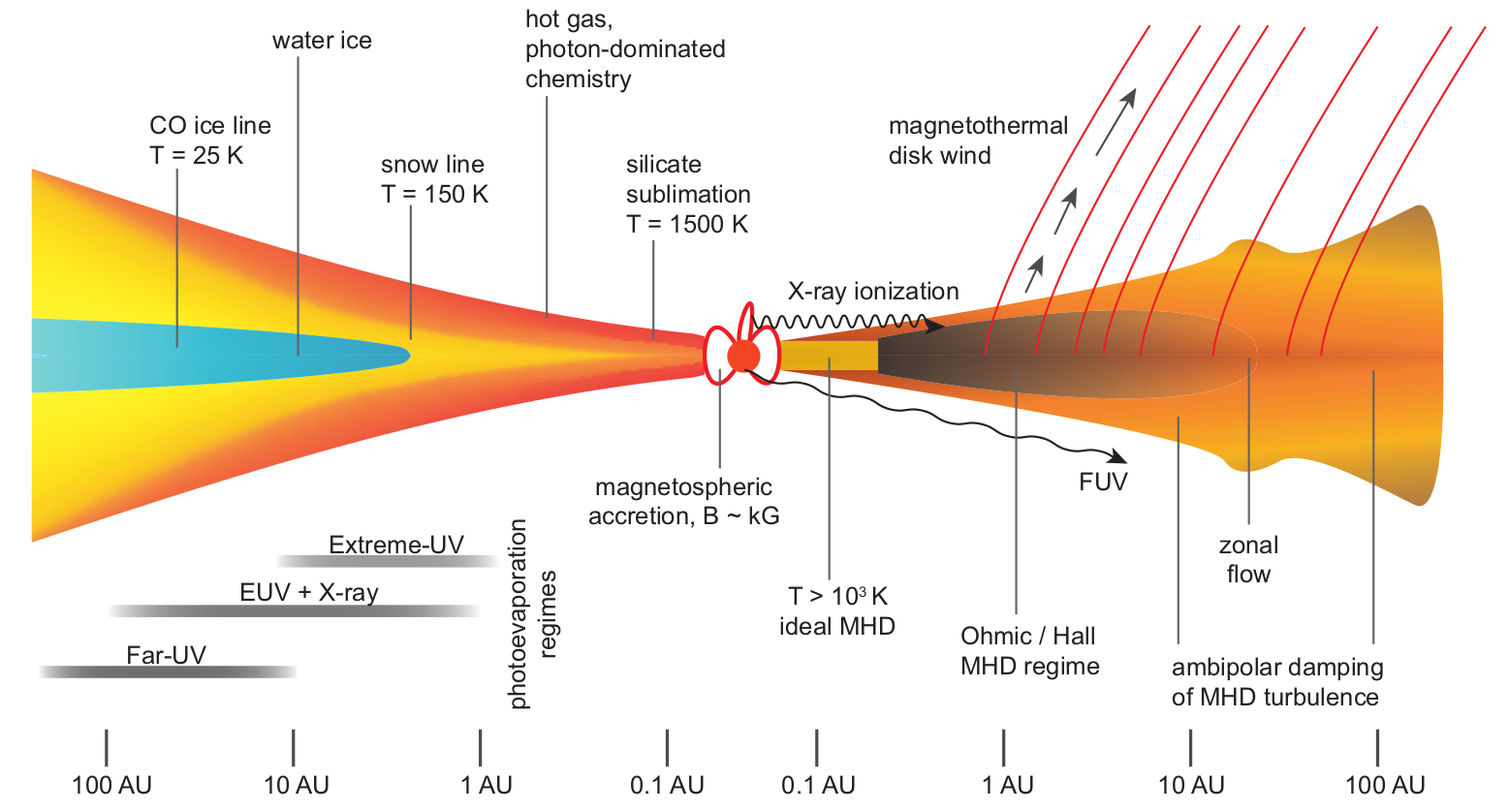

giant laboratory of fundamental
physical and chemical processes
how disks accrete; how material
is transported inwards and onto the star
Angular momentum (AM) transport
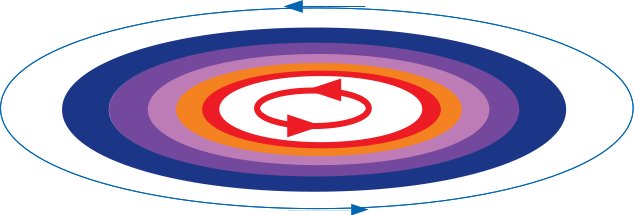
- In a Keplerian-rotating disk, rings at different radii move at different (Keplerian) velocities. This causes
shear
("friction").
The faster-moving inner rings will lose AM to the exterior ring, but gain it from the interior ring. One says that AM is being transported
- This results in a torque on the ring, which magnitude is proportional to the
(kinematic) viscosity ν.
One can derive the transport equation for the surface density:
![]()
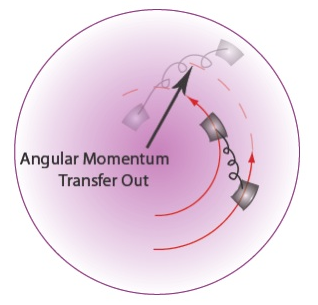
- However, the molecular viscosity is too low; an anomalous (turbulent) viscosity produced by some instability is needed. A key question is which instability provides this anomalous viscosity.

Angular momentum (AM) transport
- However, the molecular viscosity is too low; an anomalous (turbulent) viscosity produced by some instability is needed. A key question is which instability provides this anomalous viscosity.
Two leading contenders for angular momentum transport are the Magneto-rotational instability (MRI) or disk winds.

Elements of planet formation




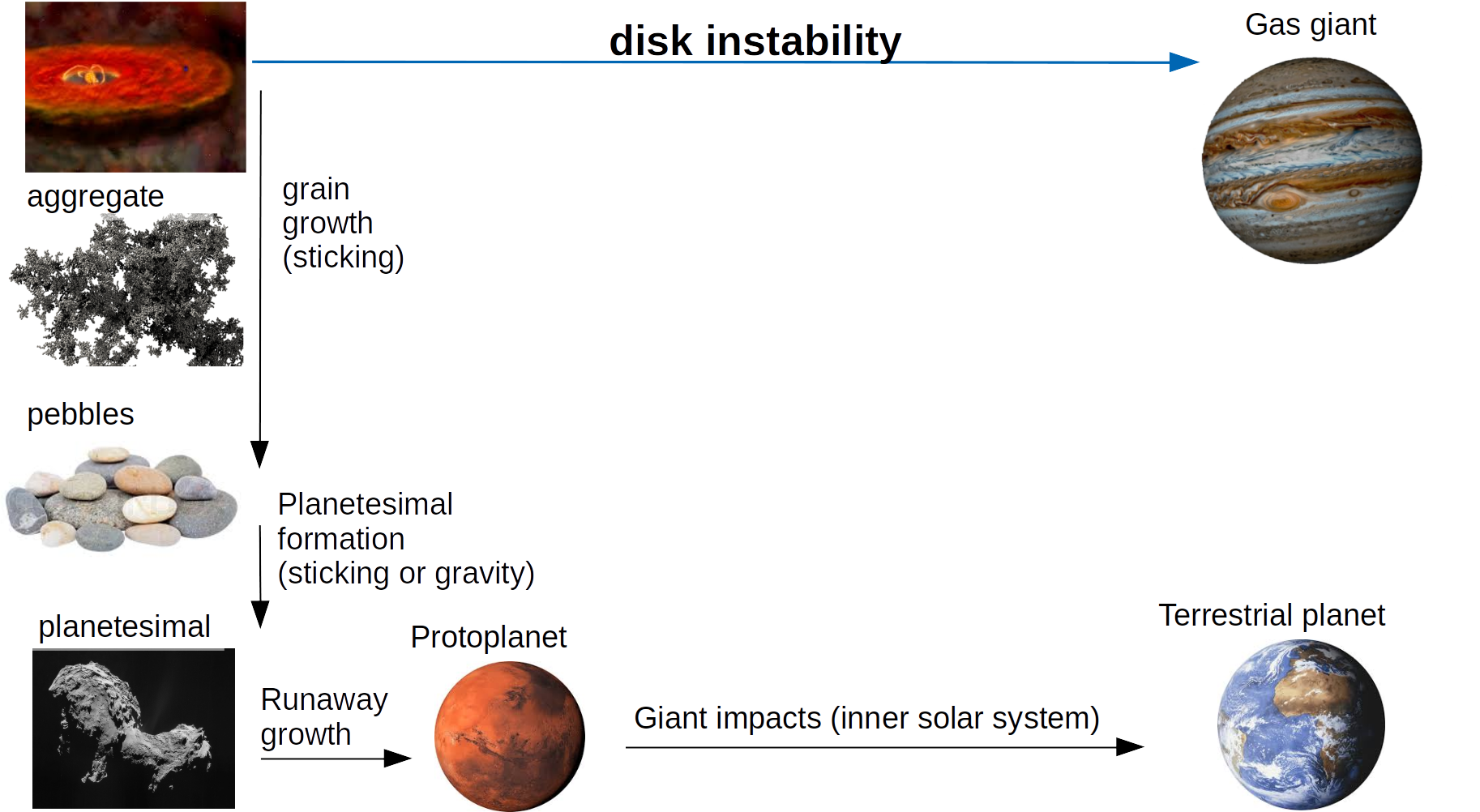
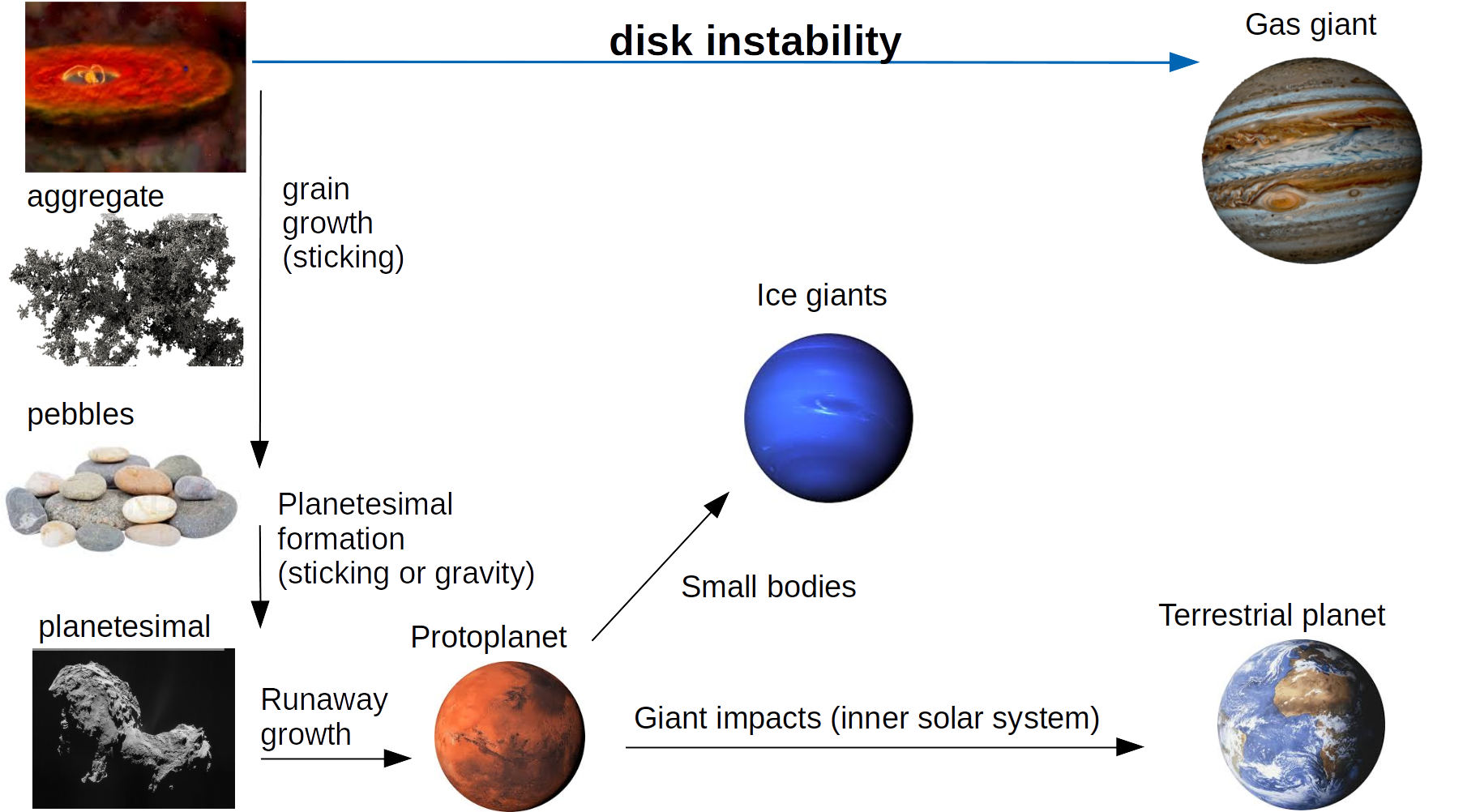
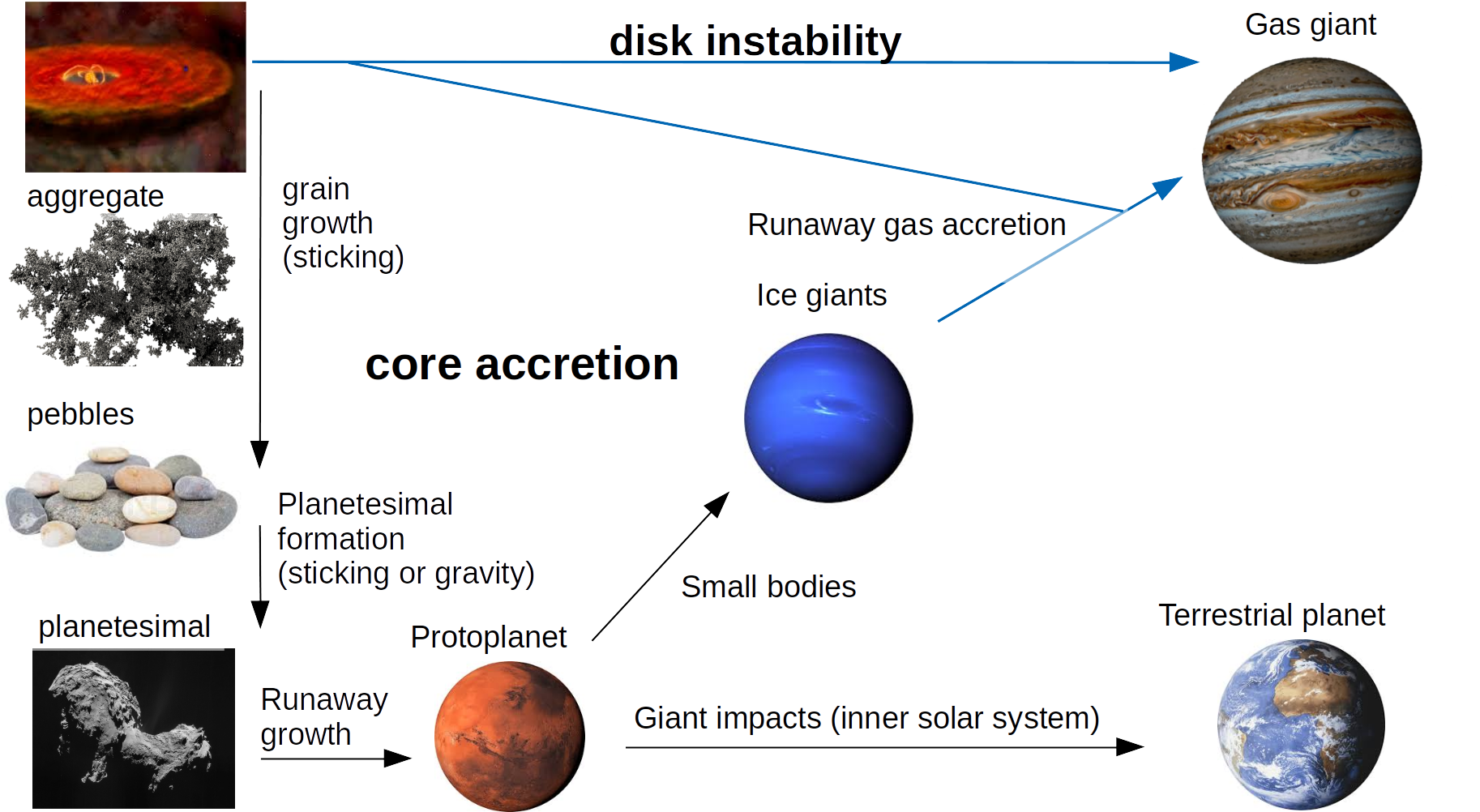
Core accretion and Disk instability
There are two main paradigms for the formation of planets:
- disk instability: planets form following a gravitational instability in the gas disk
-
core accretion:
planet formation occurs bottom-up by coagulation (collisions between solid particles)
—initially, solids stick due to surface forces
—later, bodies are held together by gravity
(at intermediate sizes sticking is problematic)

Elements of planet formation
†There are many more concepts in this field. A good reference work is Armitage (2010).
Planet formation concepts:†
- gas disk structure
gas in disks is supported by both rotation AND (a little bit) by pressure:
![]()
This means that disks are rotating slightly sub-Keplerian. This is important as it results in radial drift.
- growth timescales
- gravitational focusing
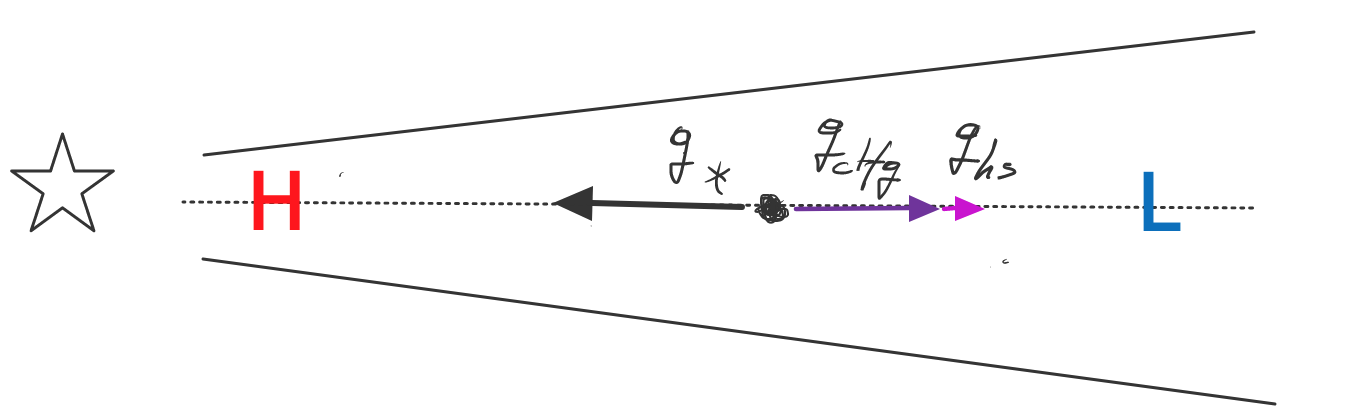
Elements of planet formation
†There are many more concepts in this field. A good reference work is Armitage (2010).
Planet formation concepts:†
- gas disk structure
- growth timescales
A simple n-σ-Δv calculation shows:
![]()
where R is the particle radius
![]() the particle internal density, ρdust the volume density in dust (or planetesimals etc.), and Δv the relative velocity.
the particle internal density, ρdust the volume density in dust (or planetesimals etc.), and Δv the relative velocity.
— growth timescales increase with distance (lower ρdust)
— growth timescales increase with size R - gravitational focusing
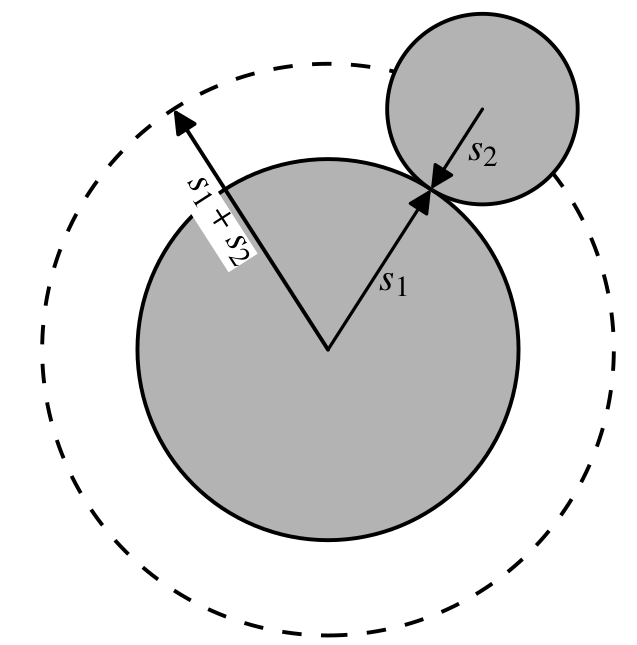
Elements of planet formation
†There are many more concepts in this field. A good reference work is Armitage (2010).
Planet formation concepts:†
- gas disk structure
- growth timescales
-
gravitational focusing
gravitational focusing greatly accelerates growth. We can obtain the collisional impact parameter
![]() by equating the angular momentum and energy at infinity and at impact:
by equating the angular momentum and energy at infinity and at impact:
![]()
this is much larger than the geometrical cross section
A consequence of gravitational focusing is that the growth time decreases,
![]() (as long as Δv remains the same), resulting in the phenomenon of
runaway growth.
(as long as Δv remains the same), resulting in the phenomenon of
runaway growth.

Planet formation challenges
(no exam material)
The core accretion model is more popular since it also explains the small bodies and terrestrial planets. Yet:
- The process is hard to observationally constrain as planet formation is rapid (~106 yr) and takes place in a dusty disk.
recent progress are high resolution observations with ALMA, and also an increasingly complete sample of exoplanets

Planet formation challenges
(no exam material)
The core accretion model is more popular since it also explains the small bodies and terrestrial planets. Yet:
- The process is hard to observationally constrain as planet formation is rapid (~106 yr) and takes place in a dusty disk.
- Collision/growth timescales are short in the inner disk, but become longer with distance to the star.
recent theoretical ideas include pressure maxima and pebble accretion
in the pebble accretion mechanism, small particles get trapped in the gravitational potential of a planet and are captured efficiently. (c) Chris Ormel.
Planet formation challenges
(no exam material)
The core accretion model is more popular since it also explains the small bodies and terrestrial planets. Yet:
- The process is hard to observationally constrain as planet formation is rapid (~106 yr) and takes place in a dusty disk.
- Collision/growth timescales are short in the inner disk, but become longer with distance to the star.
- Small grains stick due to surface forces (like vd Waals), large bodies through gravitational forces, but at intermediate scales there is no clear cohesion mechanism (meter size barrier).
it has been suggested that the problematic meter size barrier can be overcome by gravitational instability, such as the streaming instability
Planet formation challenges
(no exam material)
The core accretion model is more popular since it also explains the small bodies and terrestrial planets. Yet:
- The process is hard to observationally constrain as planet formation is rapid (~106 yr) and takes place in a dusty disk.
- Collision/growth timescales are short in the inner disk, but become longer with distance to the star.
- Small grains stick due to surface forces (like vd Waals), large bodies through gravitational forces, but at intermediate scales there is no clear cohesion mechanism (meter size barrier).
- Particles as well as planets tend to migrate on short timescales, because of aerodynamic and gravitational drag forces.
planet migration may explain the close-in planet population, but it is unclear how significant disk migration is (and how to avoid it)
end of module 4
—congrats—





















































