Stars and Planets

—Matter under astrophysical conditions—
Chris Ormel

Roadmap module 3
Mean molecular weight
(for a gas) The relation between mass density and number density
Hydrostatic Balance
The law that connects pressure to gravity
Equation of State (EoS)
derived from the Pressure Integral.
An Equation of State (EoS) describes the relationship between pressure, density and temperature.
The EoS is essential for understanding the interiors of stars (and planets)
Polytropes
Objects with an EoS P~ρ1+1/n obey a self-similar density structure. Many objects in Astronomy (White Dwarfs, neutral stars, some stars, planets) can be described as polytropes
Nuclear Fusion
The energy source that powers stars. Which physical principles underpin this essential energy source? What factors determine the energy production by nuclear fusion?
Stellar Nuclear Synthesis
How are heavy atomic nuclei produced from lighter ones?
- Fermi/Boltzmann distribution
- Ideal Eos
- (rel.)elec.deg. EoS
- radiation Eos
- Mass-radius relationships WD
- Chandrasekhar mass
- Gamow peak
- pp-chain, CNO cycle, Triple-α process
- s-process
- r-process

dominate by mass
of hydrogen is often denoted as X.
Here X=0.75
Here Y=0.23
referred to as "metals" Z. Here Z=0.02
set after the big bang
(cosmic nucleosynthesis).
Metals are produced in stars by nuclear fusion
(stellar nucleosynthesis)
astronomy periodic table
- stars' composition follow cosmic abundances
![]()
- enrichment of the ISM (interstellar medium), increase Z with time
- population III stars (hypothesized) — formed directly after the big bang. No metals.
- population II stars — old stars. Few metals
- population I stars — metal-rich. Like our Sun
for planets, the contribution of metals to their composition is much higher
Blackboard
- Equations of State (dimensionless)
- Pressure Integral
- Electron degeneracy
- Mean molecular weight
mean molecular weight
(read CO Ch.10.2, p288-296)
We define the atomic weight for a particle type X as:

 is the atomic mass units (
is the atomic mass units (
 proton mass). The atomic weight is simply the average mass of the medium per particle type X in units of
proton mass). The atomic weight is simply the average mass of the medium per particle type X in units of
 "Common particle" types are:
ions (
"Common particle" types are:
ions (
 ) and electrons (
) and electrons (
 ). Very often, e.g., if there is only one particle type the index is dropped (
). Very often, e.g., if there is only one particle type the index is dropped (
 ). Same for the total.
). Same for the total.
With this definition, we can write the number density of particle type X as:

| species | type X | M/mu | NX | μX |
|---|---|---|---|---|
| molecular hydrogen | molecules | 2 | 1 | 2 |
| ionized hydrogen | ions | 1 | 1 | 1 |
| ionized hydrogen | electrons | 1 | 1 | 1 |
| ionized hydrogen | total | 1 | 2 | 0.5 |
| ionized helium | ions | 4 | 1 | 4 |
| ionized helium | electrons | 4 | 2 | 2 |
| ionized metal | ions | 2Z | 1 | 2Z |
| ionized metal | electrons | 2Z | Z | 2 |
Common examples
mean molecular weight
If there are multiple species in the mixture, we define the Mean molecular weight μ as:

 is the number density of type X of particle species j and
is the number density of type X of particle species j and
 is the weight fraction of the species in the mixture.
is the weight fraction of the species in the mixture.

where Aj is the mass number and Zj the atomic number. It follows that for a fully ionized gas of hydrogen (X), helium (Y) and metals (Z)

| species | type X | M/mu | NX | μX |
|---|---|---|---|---|
| molecular hydrogen | molecules | 2 | 1 | 2 |
| ionized hydrogen | ions | 1 | 1 | 1 |
| ionized hydrogen | electrons | 1 | 1 | 1 |
| ionized hydrogen | total | 1 | 2 | 0.5 |
| ionized helium | ions | 4 | 1 | 4 |
| ionized helium | electrons | 4 | 2 | 2 |
| ionized metal | ions | 2Z | 1 | 2Z |
| ionized metal | electrons | 2Z | Z | 2 |
Common examples
- What is μ for Earth's atmosphere?
- What is μ for the Sun?
- What is μe for a White Dwarf?
EOS (Equation of State)
Pressure integral:

where f(p)dp is the number density of particles with momenta [p,p+dp]
with the Maxwell-Boltzmann distribution

where n is the number density.
This results in the ideal gas law:

- with mu the atomic mass unit
![]()
- nonrelativistic motion particles
- particles interact only through collisions (no long-range electrostatic forces)
- no internal structure (excitation)
EoS — Degenerate pressure
(read CO Ch16.3 p. 563-569)
Fermi distribution (electrons). For low temperature and/or high density, instead

This follows from the Pauli exclusion principle. Let

be the number of particles in 6D cell
 Pauli exclusion principle states that there are at most 2 ways to occupy these quantum cells:
Pauli exclusion principle states that there are at most 2 ways to occupy these quantum cells:

Note that in terms of spherical shell momenta d3p = 4πp2dp. The Fermi distribution limits the classical (Boltzmann) distribution (which can become arbitrarily high as it scales with ne!)

 The Fermi momentum is
The Fermi momentum is
 In the degenerate case, electrons are prevented from filling low-momenta states, providing a much higher pressure than the classical limit for low temperature or high density.
In the degenerate case, electrons are prevented from filling low-momenta states, providing a much higher pressure than the classical limit for low temperature or high density.
EoS — Degenerate pressure
Fully degenerate electron gas
- non-relativistic, degenerate:
![]()
- relativistic degenerate:
![]()
Non-relativistic and relativistic limits. The term in the [] is the electron number density ne.
Radiation Pressure. We can derive:


 The Fermi momentum is
The Fermi momentum is
 In the degenerate case, electrons are prevented from filling low-momenta states, providing a much higher pressure than the classical limit for low temperature or high density.
In the degenerate case, electrons are prevented from filling low-momenta states, providing a much higher pressure than the classical limit for low temperature or high density.
EoS (Equation of State)
With these crude expression, we identify several regions:
- radiation pressure at high temperatures.
Stars are unstable in this region (why?)
- ideal gas in the intermediate regions
this holds for stars like the Sun through much of their life
- at low temperatures and high densities pressure is dominated by degenerate electrons
- non-relativistic degeneracy
- relativistic degeneracy
electron degeneracy is important for White Dwarfs and (sometimes) the cores of stars

Blackboard
- Hydrostatic balance
- Polytropes
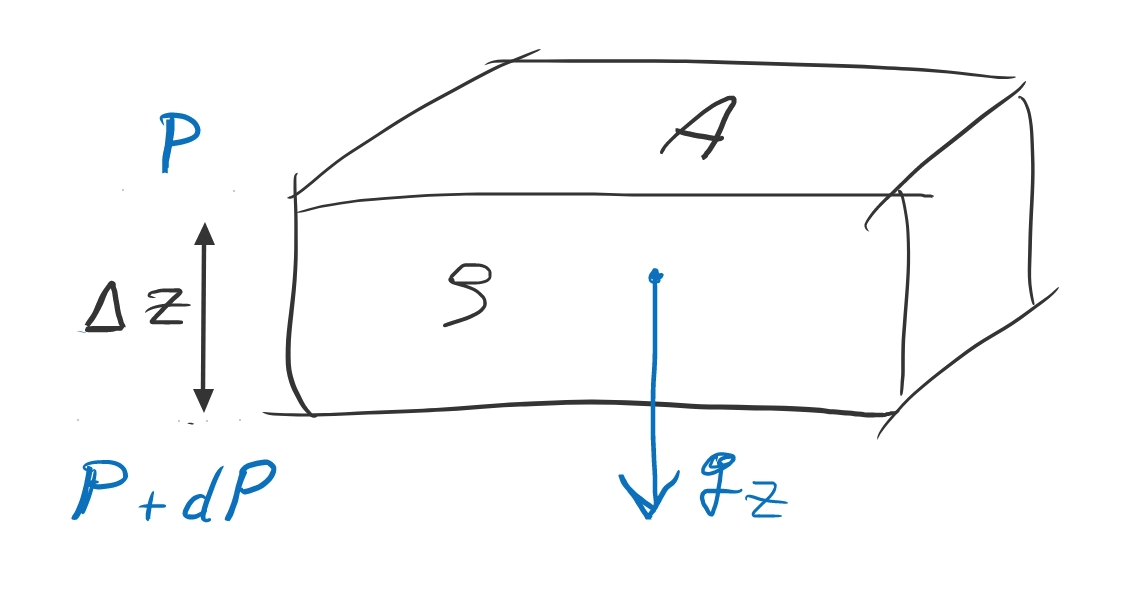
hydrostatic balance & mass conservation
(read CO Ch10.1 p. 284-288)
hydrostatic balance governs the structure of many astrophysical objects (stars, planets, gas clouds, disks) at rest

where P is pressure, ρ density, gs the gravitational acceleration along the s-dimension. One may also speak of a hydrostatic (pressure gradient) force, or acceleration ghs. In vector notation:

mass conservation (in spherical geometry) implies that

where dm is the mass of the mass shell. As an aside, for fluids, the more general mass continuity equation reads:

Polytropes
(read CO p. 334-340)
Often, the equation of state can be approximated as a polytrope

where n is the polytropic index and K a constant.
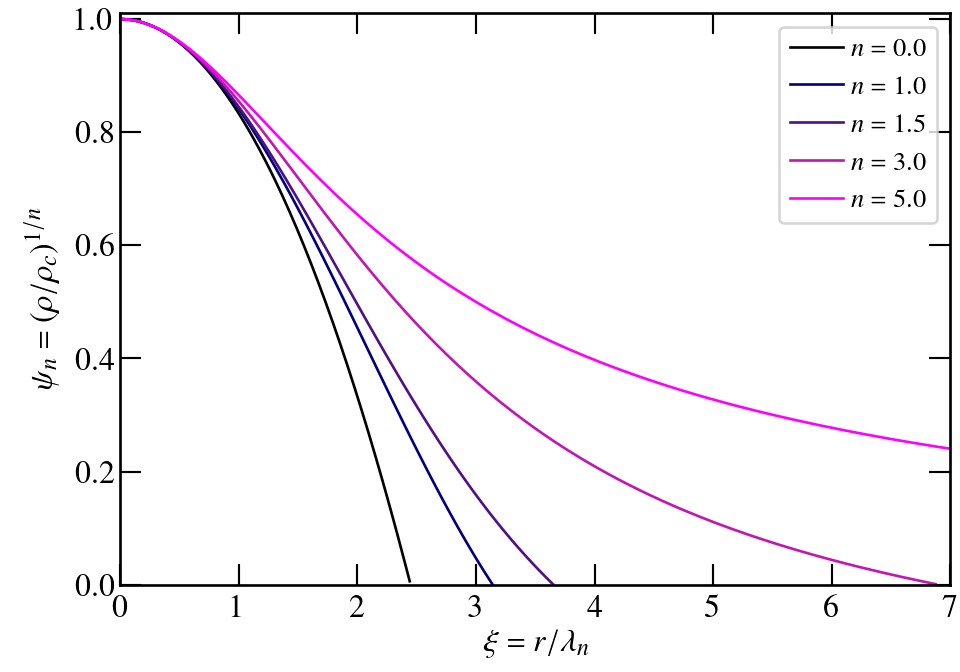
Hydrostatic balance and mass conservation result in the Lane-Emden equations

where
 the central density, and the radius has been nondimensionalized as:
the central density, and the radius has been nondimensionalized as:

Polytropes
Hydrostatic balance and mass conservation result in the Lane-Emden equations

This ordinary differential equation needs two boundary conditions:
-
![]() (by definition)
(by definition)
-
![]() (why?)
(why?)
Only n=0, 1, and 5 have analytic solutions.

others are found by numerical integration

Polytropes
numerically, solve it by writing it as a system of first order equations

import scipy.integrate as sciint
import numpy as np
#
def dy_dx (y, x, n=1):
F, psi = y
F_x = -x**2 *psi**n
if x<1e-5:
psi_x = x/3 #avoid singularity
else:
psi_x = F/x**2
return F_x, psi_x
#
#initial conditions for (F,psi)
y0 = [0,1]
yout = sciint.odeint(dy_dx, y0, xarr, args=(n,))
simple python implementation by your instructor. Here I have used scipy.integrate.odeint to let the computer do the hard work. The only tricky issue is that ψ'(x) is undefined (0/0) for x=0.
I strongly encourage you to reproduce these results.

Polytropes
Properties of polytropes
- central-to-average density:
![]()
where ξR is the value of ξ where ψn becomes zero (outer radius)
- Mass-radius relationship:
![]()
where Nn is a numerical constant.
- Central pressure—density relationship:
![]()
As Cn turns out to be similar for each n, this is a very general relation for the conditions at the center of objects in hydrostatic balance
| n | rn | Nn | Wn | Cn | applications |
|---|---|---|---|---|---|
| 0 | 1.0 | 0.119 | 0.806 | (incompressible) rocky planets | |
| 0.5—1 | neutron stars | ||||
| 1 | 3.29 | 0.637 | 0.393 | 0.542 | |
| 3/2 | 5.99 | 0.424 | 0.770 | 0.478 | — convective stars — White Dwarfs |
| 2 | 11.4 | 0.365 | 1.638 | 0.431 | |
| 3 | 54.2 | 0.364 | 11.05 | 0.364 | — Eddington solar standard model — cores White Dwarfs |
| 5 | ∞ | ∞ | ∞ | 0.269 | Plummer model stellar cluster |
| ∞ | isothermal E.o.S. | ||||
↑ Proportionality constants appearing in relationships involving mean and central density (ρc), mass M, radius R, and central pressure Pc for polytropes for selected polytropic indices n. In particular, note that N and C only weakly depend on n.
Polytropes
(read CO Ch16.4 p. 569-572)
Application of polytropes
- For n=3/2 we obtain from the mass-radius relationship:
![]()
This holds for White Dwarfs (K is a true constant). The more massive the WD, the smaller it is!
- For n=3 the radius dependence vanishes; applied to the K of the ER-degeneracy, we obtain the
Chandrasekhar mass:
![]()
which is the the maximum mass a degenerate object may have. As White Dwarfs have μe=2,
![]()
The Chandrasekhar mass is the highest mass up to which degenerate objects (White dwarfs) can exist. A star with M>MCh must collapse under its own gravity
| n | rn | Nn | Wn | Cn | applications |
|---|---|---|---|---|---|
| 0 | 1.0 | 0.119 | 0.806 | (incompressible) rocky planets | |
| 0.5—1 | neutron stars | ||||
| 1 | 3.29 | 0.637 | 0.393 | 0.542 | |
| 3/2 | 5.99 | 0.424 | 0.770 | 0.478 | — convective stars — White Dwarfs |
| 2 | 11.4 | 0.365 | 1.638 | 0.431 | |
| 3 | 54.2 | 0.364 | 11.05 | 0.364 | — Eddington solar standard model — cores White Dwarfs |
| 5 | ∞ | ∞ | ∞ | 0.269 | Plummer model stellar cluster |
| ∞ | isothermal E.o.S. | ||||
↑ Proportionality constants appearing in relationships involving mean and central density (ρc), mass M, radius R, and central pressure Pc for polytropes for selected polytropic indices n. In particular, note that N and C only weakly depend on n.
Polytropes
Caution!
- Meaning of K:
- constant K (e.g., White Dwarfs)
K is some function of fundamental constant as, e.g., with White Dwarfs. There is a unique mass-radii relationship.
- variable K (e.g., main-sequence stars)
Now K is constant for a single star, but not among stars with different mass. All scaling relationships still hold, but there is no unique mass-radius relationship.
For example, we will see in M4 that for radiatively envelopes,
![]() with the proportionality constant determined by luminosity, opacity, etc, that differs among stars. With the ideal gas law, this gives
with the proportionality constant determined by luminosity, opacity, etc, that differs among stars. With the ideal gas law, this gives
![]() and hence
and hence
![]() with the prefactor
with the prefactor
![]() varying among stars. But if
varying among stars. But if
![]() is a function of mass only, we can still obtain a mass-radius relationship.
is a function of mass only, we can still obtain a mass-radius relationship.
- constant K (e.g., White Dwarfs)
- The polytropic assumption (cnst n) will fail.
- White Dwarfs may have relativistically degenerate cores, non.rel.deg interiors, and a thin atmosphere where the ideal EoS applies. n is not constant throughout the star.
- Material may be in a partial degenerate state.
- MS-stars may have radiative interiors, convective cores, etc.
| n | rn | Nn | Wn | Cn | applications |
|---|---|---|---|---|---|
| 0 | 1.0 | 0.119 | 0.806 | (incompressible) rocky planets | |
| 0.5—1 | neutron stars | ||||
| 1 | 3.29 | 0.637 | 0.393 | 0.542 | |
| 3/2 | 5.99 | 0.424 | 0.770 | 0.478 | — convective stars — White Dwarfs |
| 2 | 11.4 | 0.365 | 1.638 | 0.431 | |
| 3 | 54.2 | 0.364 | 11.05 | 0.364 | — Eddington solar standard model — cores White Dwarfs |
| 5 | ∞ | ∞ | ∞ | 0.269 | Plummer model stellar cluster |
| ∞ | isothermal E.o.S. | ||||
← Polytropes are a useful analytical tool, but in reality calculations are done numerically.
Blackboard
- Energy sources
- Nuclear fusion
Nuclear Fusion
— read CO Ch 10.3 —
Energy reservoirs:
- Chemical:
![]()
- Gravitational (Kelvin-Helmholtz)
![]()
- Nuclear
![]()
The corresponding timescales —
 — are known as the
— are known as the
- chemical,
- Kelvin-Helmholtz contraction,
- nuclear
timescales respectively.
Physics of fusion — Tunneling
Tunneling probability. Temperatures at the center of the Sun (~107 K) are not high enough to overcome the Coulomb barrier. But nuclei can quantum-mechanically tunnel at a probability

(WKB approximation; See any textbook on quantummechanics, e.g., Griffiths.) where p denotes momentum, rE is the distance corresponding to the Coulomb barrier at given energy E and rs the distance where the strong nuclear force appears,

is the energy scale where the
de Broglie wavelength
 and Coulomb potential meet, with mμ is the reduced mass.
and Coulomb potential meet, with mμ is the reduced mass.

Physics of fusion — Reaction rate
Reaction rate — the number of reactions per unit volume per unit time — follows from an n-σ-v argument:

where n1, n2 are the number densities of the reactants, v12 the relative velocity, and σ12 the cross section for the reaction. In the second step we have introduced a distribution (and dropped indices).
The nuclear cross section
 is given by the de Broglie wavelength and the tunneling probability:
is given by the de Broglie wavelength and the tunneling probability:

where
 encapsulates all subtleties that come with a more rigorous treatment — like resonances. Essentially, this factor should be measured.
encapsulates all subtleties that come with a more rigorous treatment — like resonances. Essentially, this factor should be measured.
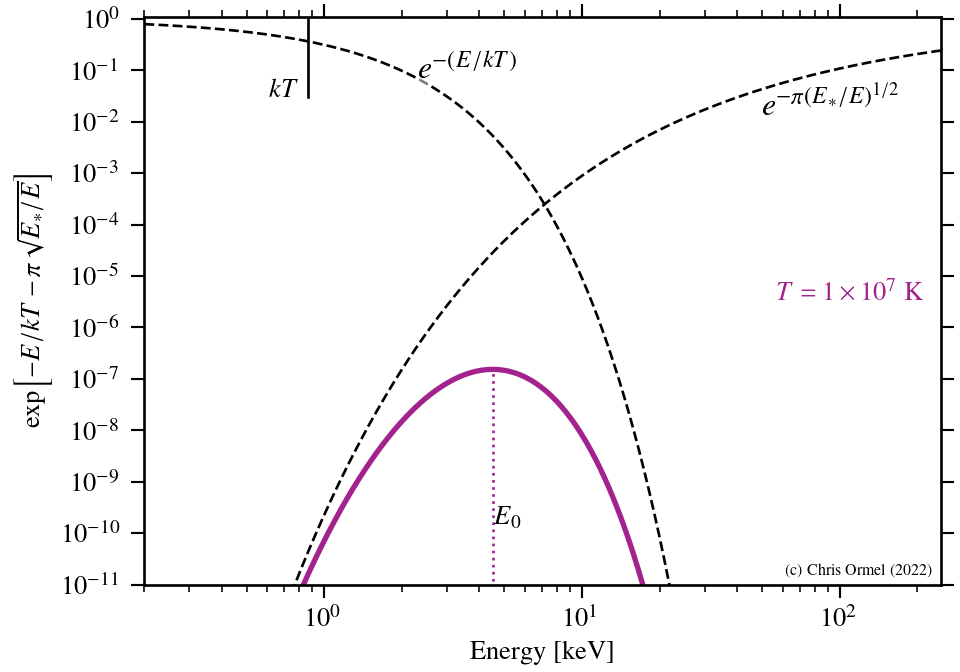
The Gamow peak arises at the point where the Boltzmann factor — the probability of particles in the distribution — and the tunnelling probability "meet".
Physics of fusion — Reaction rate
Reaction rate — the number of reactions per unit volume per unit time — follows from an n-σ-v argument:

Inserting for
 ,
,
 , and
, and
 :
:

where for f(E) we have inserted the Boltzmann energy distribution.
The largest contributions arises from the energies where the argument of the exponent is smallest. This is known as the Gamow peak.

The Gamow peak arises at the point where the Boltzmann factor — the probability of particles in the distribution — and the tunnelling probability "meet".
Physics of fusion — Reaction rate
Reaction rate

The largest contributions arises from the energies where the argument of the exponent is smallest. This is known as the Gamow peak.
- Only high-energy nuclei can fuse!
- Nuclear reaction rate very sensitive to temperature!
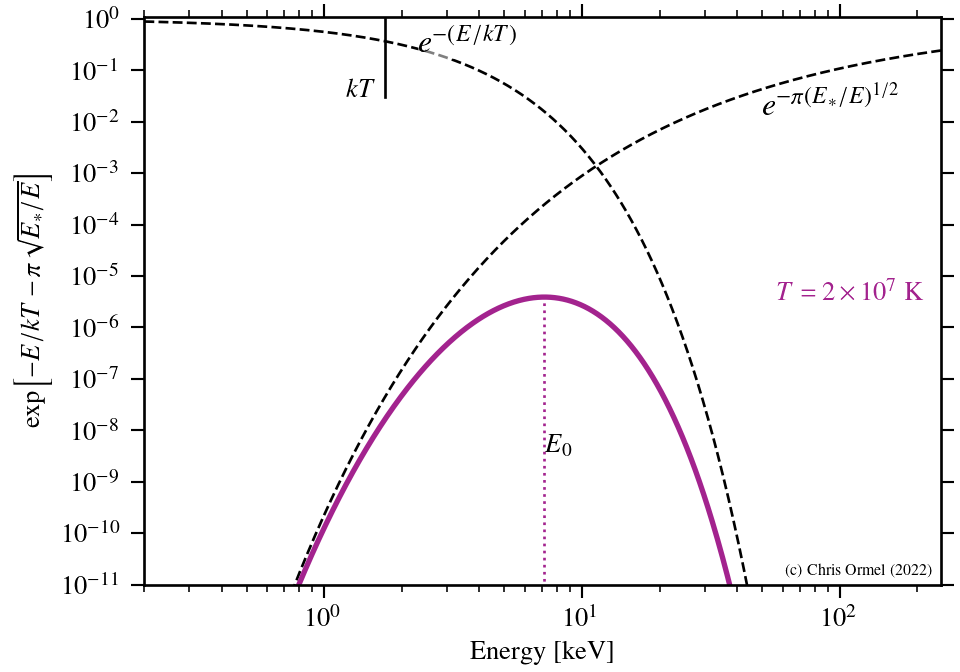
The Gamow peak arises at the point where the Boltzmann factor — the probability of particles in the distribution — and the tunnelling probability "meet".
Stellar Nucleosynthesis
- H-fusion. The net reaction is
![]()
- This net reaction can be accomplished through the
proton-proton (PP) chain:
(a)
![]()
- Other variations of the PP-chain exist. This is the dominant pathway for the Sun.
- There's an important catch to the first (rate-limiting) reaction, which is a combination of proton fusion and
β-decay
of one of the protons:
![]()
but the last reaction (β-decay) is very unlikely. In most of the times the diproton just fissions back to two protons. The β-decay is the rate-limiting step
- Deuterium burning.
- This net reaction can be accomplished through the
proton-proton (PP) chain:
(a)

Stellar Nucleosynthesis
- H-fusion. The net reaction is
![]()
- This net reaction can be accomplished through the proton-proton (PP) chain:
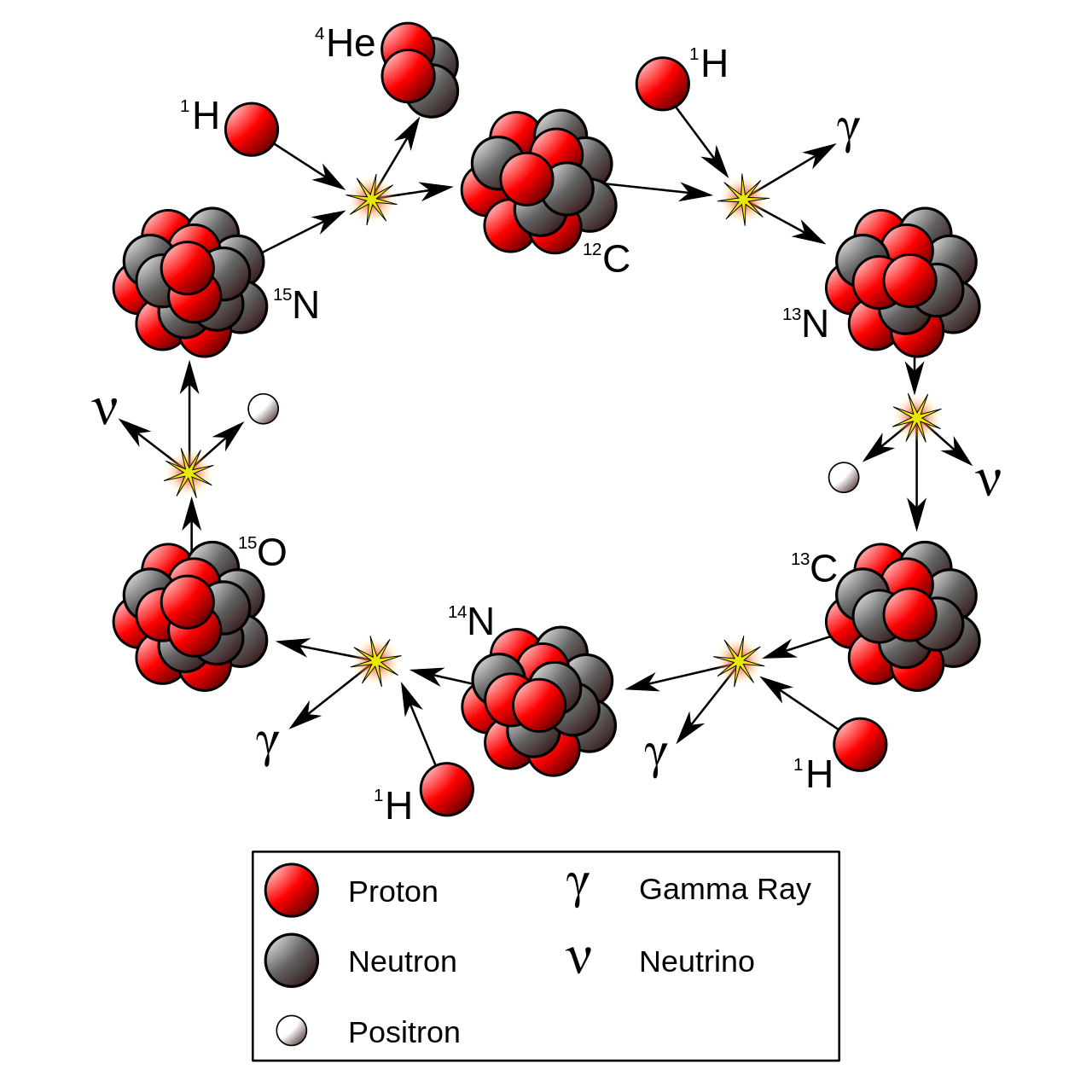
- Another way to achieve the same net result is the
CNO cycle:
![]()
† this is the rate-limiting step
Stellar Nucleosynthesis
- H-fusion. The net reaction is
![]()
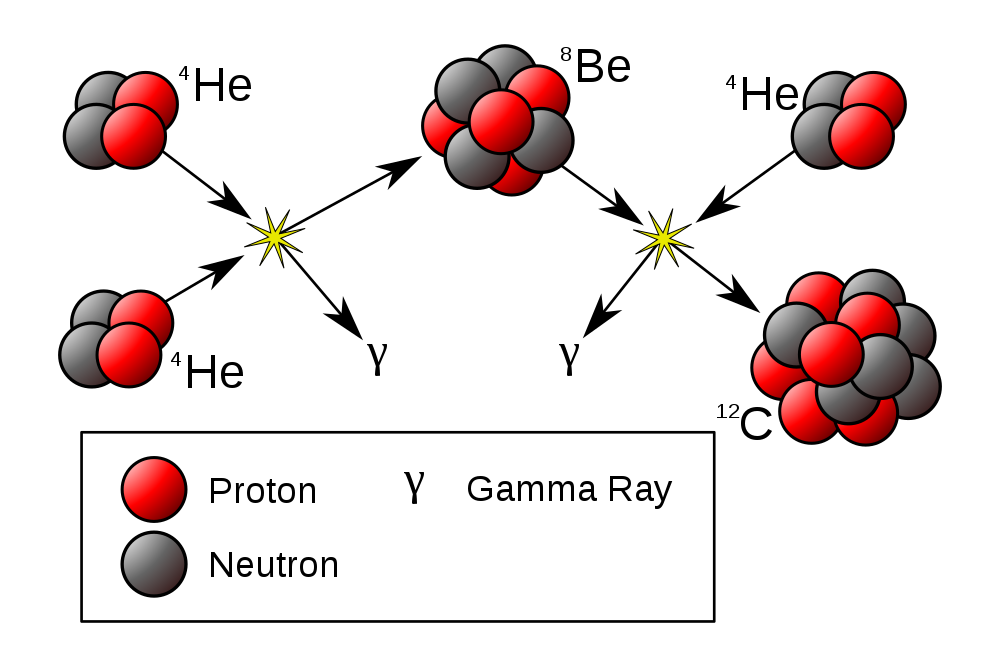
- He-fusion. In the
triple alpha process,
He-nuclei fuse into carbon
![]()
Stellar Nucleosynthesis

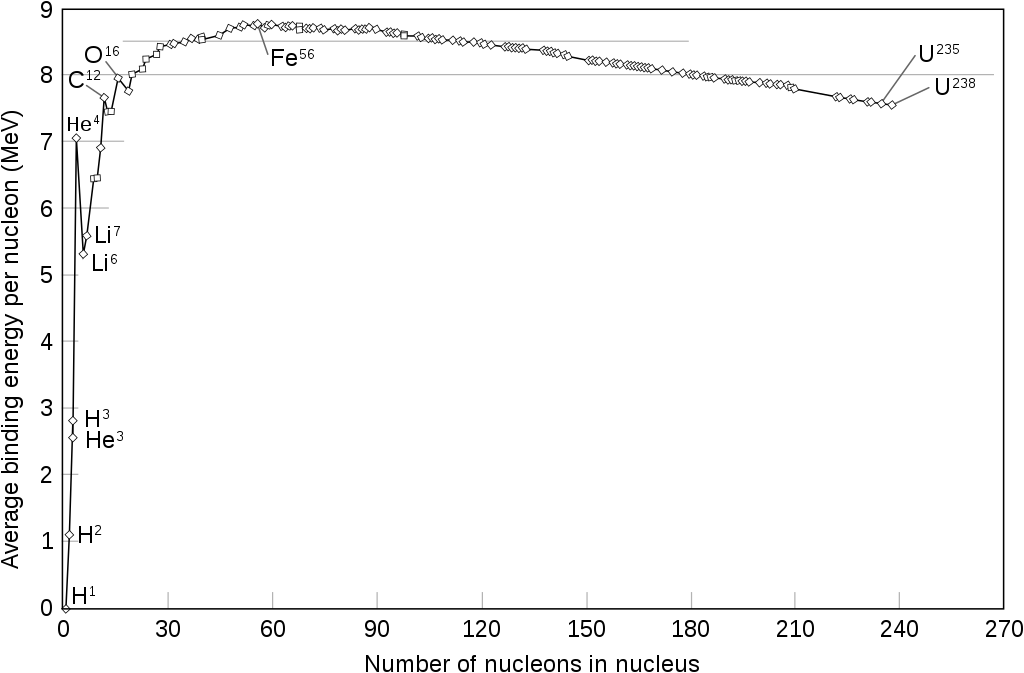
Nuclear binding energy Eb is energy that is released by building the nucleus from its constituents.
— mp, mn: mass of proton, neutron
— A: total number of nucleons (mass number)
— Z: total number of protons (atomic number)
— mnucl: actual (measured) mass of the nucleus
— c: speed of light
Stars on the main-sequence convert H into He-4, liberating large amount of energy!
Stellar Nucleosynthesis

After He, heavier elements can be formed if temperatures are high enough:
-
![]() (triple-alpha process)
(triple-alpha process)
- On to Fe-56 (high mass star)
Heavy elements ("Z") are returned to the ISM by winds during the AGB phase and supernovae explosions:
you are made from stardust
Stellar Nucleosynthesis
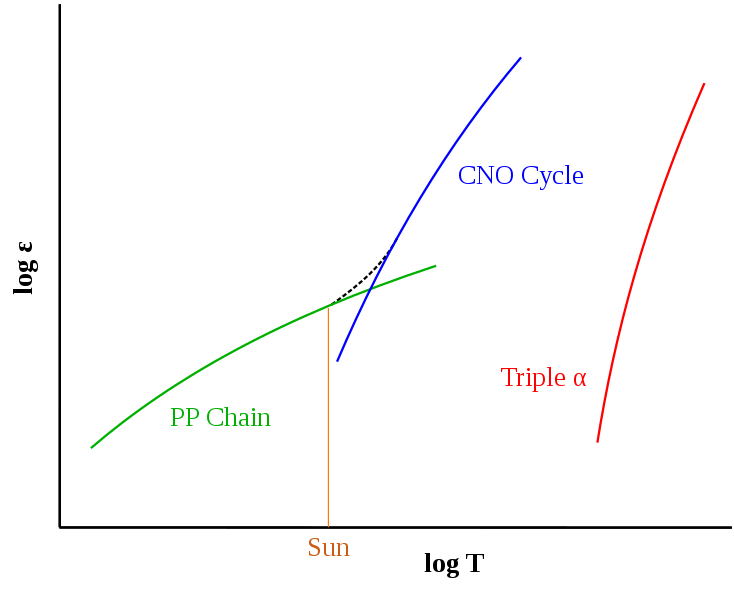
nuclear reaction rates feature a very strong dependence on temperature

Given this extreme T-dependence, shouldn't stars (and the Sun) "explode"? Why don't they "explode"?
end of module 3
—congrats—