Stars and Planets

< < Module 6 > >

—Atmospheres—

Chris Ormel

Roadmap module 6

Transitions

The change of an atom or molecule to a different energy state, which can result in the formation of a spectral line

→
↓ | |

(atomic) Hydrogen spectrum

Lyman, Balmer, Paschen, ... series

↓ |

Stellar classification

characterize stars by their spectrum. O, B, A, F, G, K, M

↑ |

(collisional) Ionization and excitation

Boltmann (excitation) and Saha (inonization) equations together determine the level populations of energy states

  ↓

(exo)Planet atmospheres

Transparancy (size) atmosphere varies at different wavelengths

→

  • electronic transitions
  • vibrational transitions
  • molecular transitions
  • transmission spectrum
  • greenhouse effect

Topics

  • electronic/vibrational/molecular
  • Saha equation
  • Planet atmospheres

Transitions

read CO Ch. 8.1

  • Electronic. Following Bohr's classical atomic model, energy levels for the electron are discretized as

    where with the Bohr radius. This correspond to energy levels with transitions occurring at near-UV/visible wavelengths.

  • Vibrational. Energy levels are

    where v is the vibrational quantum number and the frequency is related to the bond force constant k (Hooke's law) . Energy levels a factor lower than electronic. Lines appear at near-IR wavelengths

  • Rotational. Energy levels are

    (valid for a rigid rotating diatomic or linear molecule), where I is the moment of inertial and J is the rotational quantum number. Energy levels are lower by compared to electronic. Transitions occur at (sub)millimeter wavelengths

Transitions

read CO Ch. 8.1

  • Electronic. Following Bohr's classical atomic model, energy levels for the electron are discretized as

    where with the Bohr radius. This correspond to energy levels with transitions occurring at near-UV/visible wavelengths.

  • Vibrational. Energy levels are

    where v is the vibrational quantum number and the frequency is related to the bond force constant k (Hooke's law) . Energy levels a factor lower than electronic. Lines appear at near-IR wavelengths

  • Rotational. Energy levels are

    (valid for a rigid rotating diatomic or linear molecule), where I is the moment of inertial and J is the rotational quantum number. Energy levels are lower by compared to electronic. Transitions occur at (sub)millimeter wavelengths

molecular vibration of the HCl molecule. Energy is expressed in wavenumbers. The potential is the so-called Morse potential. (c) wikipedia

Transitions

read CO Ch. 8.1

  • Electronic. Following Bohr's classical atomic model, energy levels for the electron are discretized as

    where with the Bohr radius. This correspond to energy levels with transitions occurring at near-UV/visible wavelengths.

  • Vibrational. Energy levels are

    where v is the vibrational quantum number and the frequency is related to the bond force constant k (Hooke's law) . Energy levels a factor lower than electronic. Lines appear at near-IR wavelengths

  • Rotational. Energy levels are

    (valid for a rigid rotating diatomic or linear molecule), where I is the moment of inertial and J is the rotational quantum number. Energy levels are lower by compared to electronic. Transitions occur at (sub)millimeter wavelengths

Rotational energy levels within their vibrational states. (c) Martin Kraft

 

Transitions

The transition strength is determined by:

  • the extent the upper level is populated; and
  • the rate at which the excited state will decay by photon emission (Einstein-A)

    (for an emission line).

  • Selection rules. Not all transitions are allowed.

    Dipole transitions require (i) a permanent dipole moment; and (ii) . Symmetric molecules — notably H2 — do not have a permanent dipole moment! They can emit only through much weaker quadrapule transitions . In cold disk, the gas is molecular but H2 is essentially invisible

Question:
How then do astronomers measure the mass of cold, molecular gas?

Molecules need a possess a permanent dipole to excite rotation energy levels. (c) hyperphysics

 

Transitions

The transition strength is determined by:

  • the extent the upper level is populated; and
  • the rate at which the excited state will decay by photon emission (Einstein-A)

    (for an emission line).

  • Selection rules. Not all transitions are allowed.

    Dipole transitions require (i) a permanent dipole moment; and (ii) . Symmetric molecules — notably H2 — do not have a permanent dipole moment! They can emit only through much weaker quadrapule transitions . In cold disk, the gas is molecular but H2 is essentially invisible

Figure on the right shows the energy levels of the CO molecule. At high temperatures — e.g., room temperatures — all levels will be occupied. But at lower T — e.g., ~10 K for molecular clouds or the interior regions of protoplanetary disks — only the lowest J levels will be.


Given the level populations and the transition rates — the Einstein-A coefficient — the line strength can be calculated.

rotational energy levels CO

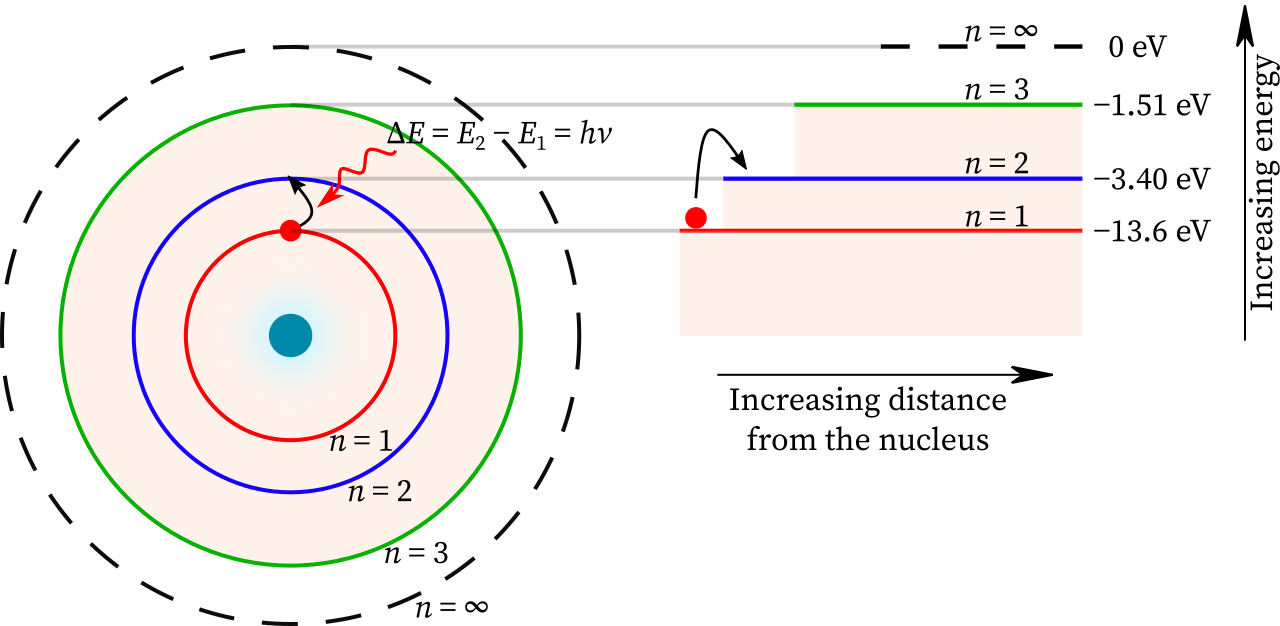
Electronic transitions/H-atom

 

  • (semi-classical) Bohr atomic model

    Bohr postulated that angular momentum of the electron is quantized in units of . The corresponding energy levels are

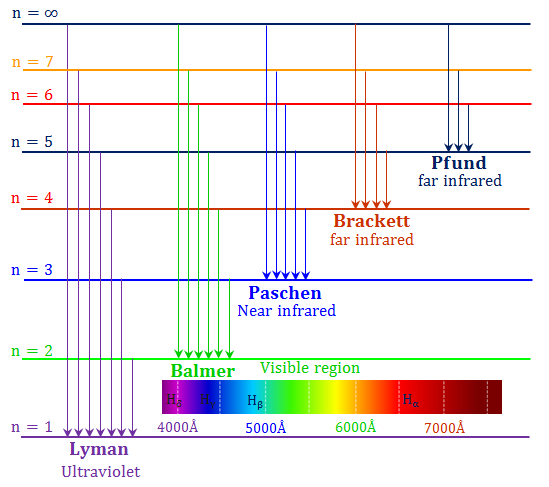
  • For the hydrogen atom, the resulting transitions give rise to lines in the UV (n=1; Lyman), Visible (n=2; Balmer) and IR

    Lines are further identified by a greek subscripts, e.g. for the transition, for the etc. The Balmer series appears in the visible.

  • In stellar atmospheres, these transitions appear in absorption
(c) https://chemistrygod.com/bohr-atomic-model
nameabbr.nrange λ [μm]
LymanLy10.0912—0.122
BalmerBa or H20.0365—0.656
PaschenPa30.821—1.88
BrackettBr41.26—4.05
PfundPf52.28—7.46
HumphreysHu63.28—12.4

Electronic transitions/H-atom

 

  • (semi-classical) Bohr atomic model

    Bohr postulated that angular momentum of the electron is quantized in units of . The corresponding energy levels are

  • For the hydrogen atom, the resulting transitions give rise to lines in the UV (n=1; Lyman), Visible (n=2; Balmer) and IR

    Lines are further identified by a greek subscripts, e.g. for the transition, for the etc. The Balmer series appears in the visible.

  • In stellar atmospheres, these transitions appear in absorption

Question:
Why in absorption?

Electronic transitions of the H atom. Note that the vertical spacing is not proportional to energy. The Balmer (H) transitions occur in the visible. (c) libretext.org

ionization

read KW. Ch 14.1—2

 

The Boltzmann equation determines the occupation levels within an ionization state

where Ei denotes the energy level with respect to the ground state (E1=0), gi the statistical weight, and Z the partition function:

ionization

read KW. Ch 14.1—2

 

The Boltzmann equation determines the occupation levels within an ionization state

The Saha equation determines the occupation levels among ionization states:

where Eion is the ionization energy, and the Zint are internal partition functions.

ionization

read KW. Ch 14.1—2

 

The Boltzmann equation determines the occupation levels within an ionization state

The Saha equation determines the occupation levels among ionization states:

Applied to the ionization of hydrogen, we obtain

where AB=HI, A=HII, B=e, , , , . is known as the ionization fraction.

Question: Do we see Balmer lines in the Sun's atmosphere?

Boltzmann and Saha distribution towards the 2nd electronic level. The black curve gives the fraction of H in the neutral state, the dashed blue curve the fraction of neutral H-atoms in the 2nd electronic level (n=2). The product of these two curves therefore gives the total fraction of H that is neutral and in the 2nd excited state (solid blue). These numbers govern the formation of Balmer lines in the photosphere of stars. 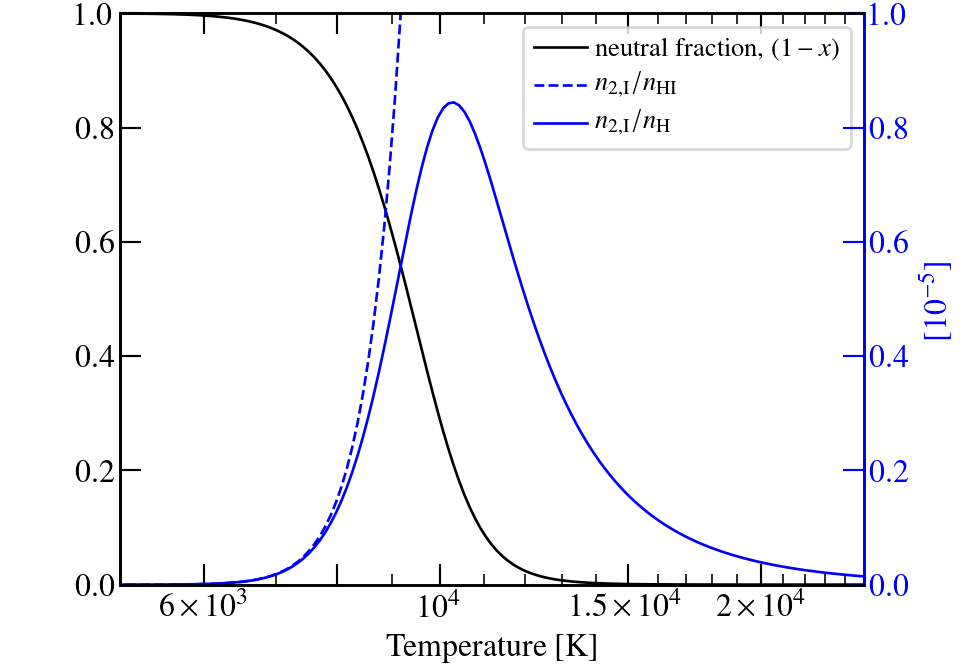A pressure of was used for all T.

ionization

read KW. Ch 14.1—2

 

The Boltzmann equation determines the occupation levels within an ionization state

The Saha equation determines the occupation levels among ionization states:

Applied to the ionization of hydrogen, we obtain

Note that in Astronomy roman numericals indicate the ionization stage:

  1. (single roman) for neutral (e.g., HI is neutral hydrogen)
  2. (roman numeral 2) for singly ionized (e.g., HII is ionized hydrogen)
  3. (roman 3) for double-ionized (e.g., OIII is O2+)
  4. etc.
Boltzmann and Saha distribution towards the 2nd electronic level. The black curve gives the fraction of H in the neutral state, the dashed blue curve the fraction of neutral H-atoms in the 2nd electronic level (n=2). The product of these two curves therefore gives the total fraction of H that is neutral and in the 2nd excited state (solid blue). These numbers govern the formation of Balmer lines in the photosphere of stars. A pressure of was used for all T.

ionization

read KW. Ch 14.1—2

 

The Boltzmann equation determines the occupation levels within an ionization state

The Saha equation determines the occupation levels among ionization states:

Applied to the ionization of hydrogen, we obtain

Pressure ionization becomes important at high densities

This occurs when with a0 the Bohr radius. Or Above these densities, everything is ionized.

Boltzmann and Saha distribution towards the 2nd electronic level. The black curve gives the fraction of H in the neutral state, the dashed blue curve the fraction of neutral H-atoms in the 2nd electronic level (n=2). The product of these two curves therefore gives the total fraction of H that is neutral and in the 2nd excited state (solid blue). These numbers govern the formation of Balmer lines in the photosphere of stars. A pressure of was used for all T.
O6.5
B0
B6
A1
A5
F0
F5
G0
G5
K0
K5
M0
M5
(c) NOIRLab/NSF/AURA
See also http://www.astronomy.ohio-state.edu/~pogge/Ast162/Unit1/SpTypes/index.html

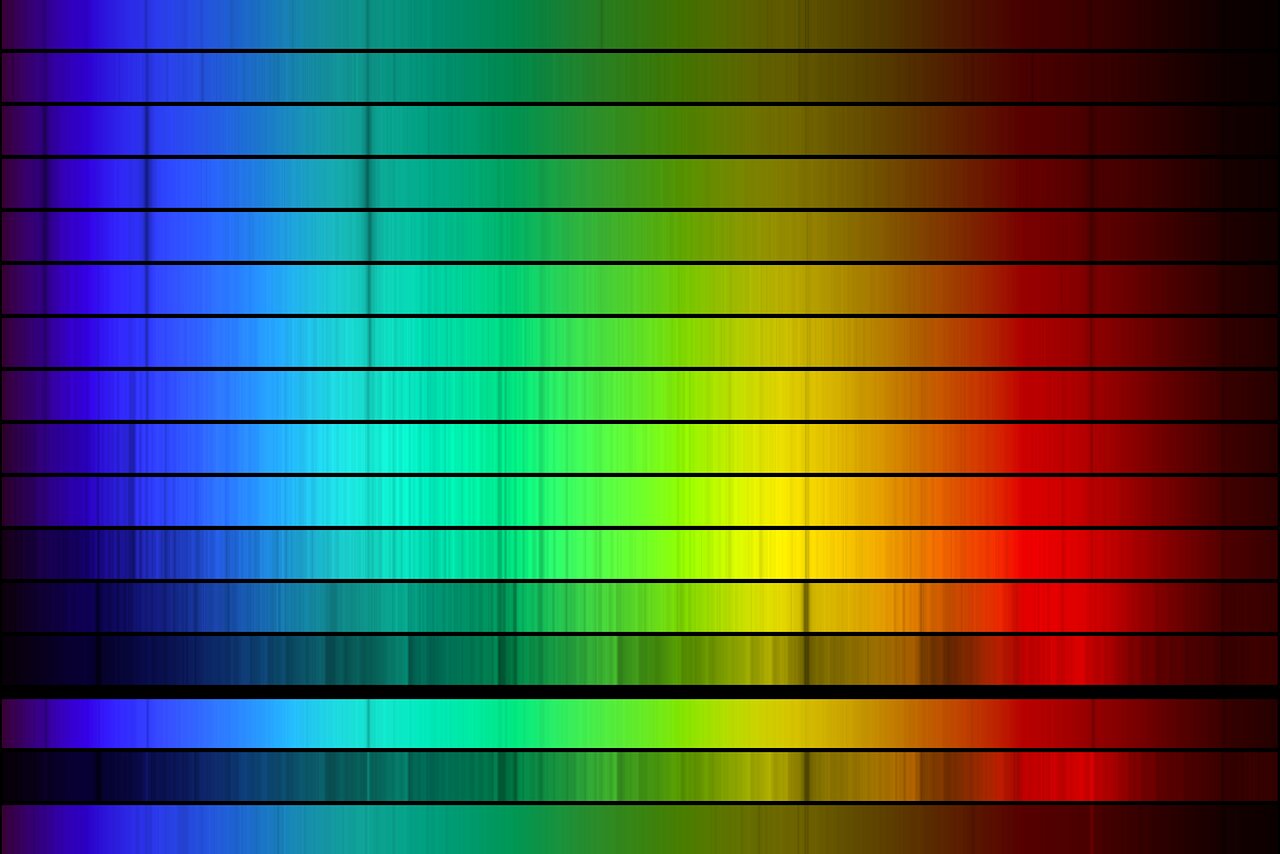
stellar classification

read CO Ch. 8

O6.5
B0
B6
A1
A5
F0
F5
G0
G5
K0
K5
M0
M5
(c) NOIRLab/NSF/AURA
See also http://www.astronomy.ohio-state.edu/~pogge/Ast162/Unit1/SpTypes/index.html
TypeT(K)Spectral lines
O>25,000Neutral and ionized He
B11,000—25,000Neutral He, some H
A7,500—11,000strong H; ionized metal (Ca II, Mg II)
F6,000—7,500weak H; ionized metal
G5,000—6,000ionized and neutral metal
K3,500—6,000strong metal
M<3,500molecules (TiO, MgH)
Stellar classes by spectral line prominence. See Table 8.1 of CO

planet atmospheres

Earth's atmosphere consist of several layers

  • exosphere. Here the particle mean free path exceeds the pressure scaleheight
  • thermosphere. Very rarified layer. The ISS and the Tiangong space station (天宫) occupy this layer at ~400 km
  • mesosphere. The energy balance is such that the temperature decreases again with height.
  • stratosphere. Contains the ozone (O3) layer. Temperature rises with height due to UV absorption (and limited cooling). Convectively stable.
  • troposphere. The lowest layer most of its mass, clouds, weather, etc. Temperature decreases with height (heated from below).

atmospheres

— read CO 19.3 —

The equilibrium temperature of a body at distance d from the star is

where a is the albedo — the amount of stellar light that is reflected. For the Earth, . However, this expression underestimate the surface temperature of the Earth, due to the greenhouse effect.


With the greenhouse effect , the surface temperature increases

where τIR is the opacity in the infrared

Note. — this is essentially the Eddington approximation

illustration of the greenhouse effect. The atmosphere is transparant to the incoming optical/UV radiation, but not to the emergent IR radiation. The radiation gets absorbed after each unit of optical depth. The greenhouse effects contributes to give a surface temperature that is higher than the irradition temperature.

atmospheres

— read CO 19.3 —

The equilibrium temperature of a body at distance d from the star is

where a is the albedo — the amount of stellar light that is reflected. For the Earth, . However, this expression underestimate the surface temperature of the Earth, due to the greenhouse effect.


With the greenhouse effect , the surface temperature increases

where τIR is the opacity in the infrared

Note. — this is essentially the Eddington approximation

(1)
(4)
(3)
(3)
(2)
(2)
(1)
(1)
illustration of the greenhouse effect. The atmosphere is transparant to the incoming optical/UV radiation, but not to the emergent IR radiation. The radiation gets absorbed after each unit of optical depth. The greenhouse effects contributes to give a surface temperature that is higher than the irradition temperature.

greenhouse effect

Outgoing thermal IR radiation trapped by vibrational transitions from molecules as CO2 and H2O!


Although the heat trapping principle is solid (it should not be disputed!), complexity arises in understanding feedback effects

  • enhanced concentration of H2O (+)
  • ice melting (+)
  • arctic methane release (thawing permafrost) (+)
  • carbon cycle (?)
  • clouds (?)

    low clouds contribute to albedo; high clouds trap IR-radiation

(c) wikimedia/Robert A. Rohde/Global Warming Art project

greenhouse effect

Outgoing thermal IR radiation trapped by vibrational transitions from molecules as CO2 and H2O!


Although the heat trapping principle is solid (it should not be disputed!), complexity arises in understanding feedback effects

  • enhanced concentration of H2O (+)
  • ice melting (+)
  • arctic methane release (thawing permafrost) (+)
  • carbon cycle (?)
  • clouds (?)

    low clouds contribute to albedo; high clouds trap IR-radiation

Venus — where the greenhouse effect entered runaway. (c) wikipedia

atmospheric escape

molecules escape at the exobase, when their velocity exceeds the escape velocity (Jeans escape). This results in a mass flux of

where is the ratio between the escape velocity and the thermal velocity

exoplanet atmospheres

  • Three types of spectra:
    • emission spectrum

      the spectrum arising from the brightness of the object itself

    • transmission spectra

      the spectrum arising when radiation of a (brighter) background object passes through a foreground object, e.g., a planetary atmosphere

    • reflection spectra

      the (stellar) light reflected by the object

  • if the planet is transiting a star, a transit spectrum can be obtained

↗ emission, transmission, and reflection (Gao et al. 2021)

→ planet size at different wavelengths. The atmosphere opacity and therefore its size depends on wavelength.

transmission spectrum

Transmission spectrum of Wasp-39b with JWST/NIRSpec (webbtelescope.org). The hot-Jupiter planet blocks about 2.1% of the stellar light, but a bit more at 4.4μm — exactly at CO2's vibrational band. Hence, the detection of carbon dioxide in this planet.

end of module 6

—congrats—