Stars and Planets

—Planet Dynamics—
Chris Ormel

Roadmap module 7
Two-body problem
The solutions of the equation of motion between two gravitating bodies.
Circular restricted Three-body problem
A special case of the three-body problem with two massive bodies on a circular orbit and a third (massless) test particle. The motion is described in the co-moving frame where the gravitating bodies are at rest.
→
Hill's approximation
Applicable when the secondary mass' is small
Tides
Deformation of an extended body by the perturber's gravity, causing energy to be dissipated
Orbital resonances
Regular, periodic forcing between planetary bodies, when conjuctions take place at similar points in the orbit
- Integrals of motion
- Kepler's equation
- Orbital elements
- Guiding center approximation
- Jacobean energy
- Lagrange points
- Roche lobe overflow
- Hill radius
- Roche limit
- Tidal quality factor
- Tidal orbital decay
- Tidal locking
- Tidal heating
- Resonance angle
- Libration
- Resonance trapping
Topics
- Two body problem
- Three body problem
- Tides
- Resonances
Two body problem
- It can be cast in terms of the relative motion
![]() and total gravitational mass
and total gravitational mass
![]()
- motion is in a plane
The two-body problem for bodies at a mass ratio
 .
↗
In the inertial frame both bodies orbit around the center of mass (cross).
↘
relative motion with one of the bodies put at the center. This representation is far more common (and useful) when
.
↗
In the inertial frame both bodies orbit around the center of mass (cross).
↘
relative motion with one of the bodies put at the center. This representation is far more common (and useful) when
 . However, motion is not in an inertial coordinate frame.
The orbit is elliptical, here with an eccentricity of e=0.7.
. However, motion is not in an inertial coordinate frame.
The orbit is elliptical, here with an eccentricity of e=0.7.
Two body problem
- It can be cast in terms of the relative motion
![]() and total gravitational mass
and total gravitational mass
![]()
- motion is in a plane
- conserved quantities:
Energy ![]()
Angular momentum ![]()
Eccentricity vector ![]()
- the orbit
![]()
![]()
which describes an ellipse with semi-major axis
![]() and semi-minor axis
and semi-minor axis
![]() .
.
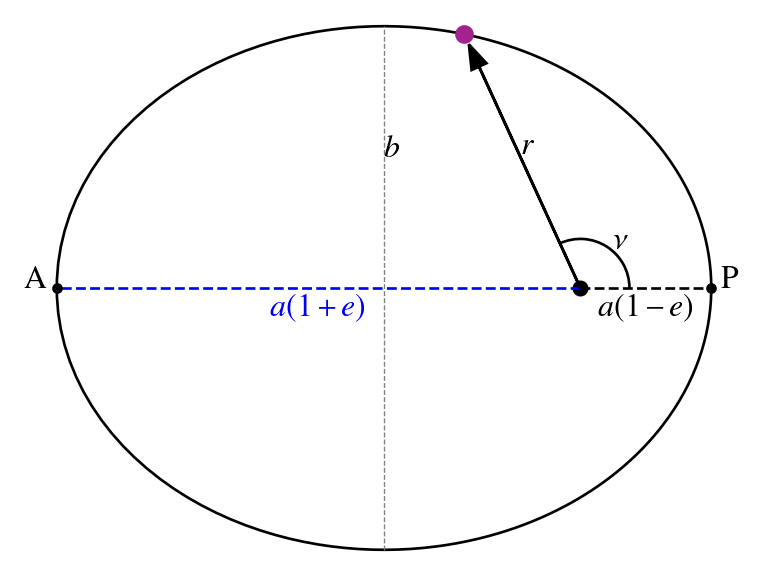
 pericenter P, apocenter A, eccentricity e.
pericenter P, apocenter A, eccentricity e.
Two body problem
- the orbit
![]()
![]()
which describes an ellipse with semi-major axis
![]() and semi-minor axis
and semi-minor axis
![]() .
.
- energy, angular momentum in terms of orbital elements:
![]()
- the orbital period
![]()
where n is the mean motion. This is Kepler's law (not to be confused with Kepler's equation [see below], which describes how
![]() is related to time
is related to time
![]() ).
).

 pericenter P, apocenter A, eccentricity e.
pericenter P, apocenter A, eccentricity e.
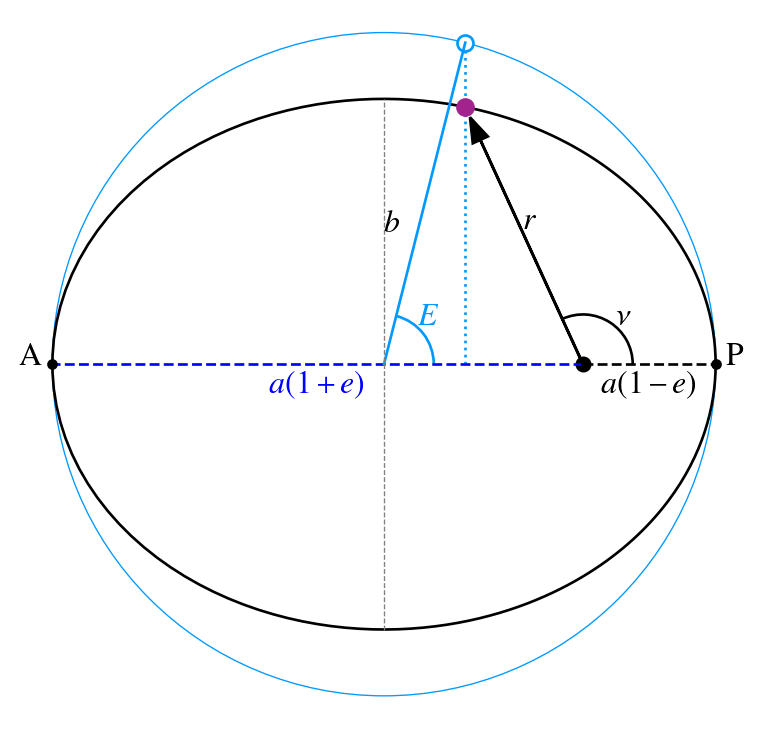
Kepler's equation
Three anomalies
-
Mean anomaly
(time),
![]()
where t is time, n the mean motion, and t0 the time of pericenter passage
-
True anomaly
![]()
indicates the position of the particle in the orbit
-
Eccentric anomaly
E
another indicator for the position of the orbit (see figure) the eccentric and true anomalies are geometrically related:
![]()
Kepler's equation relates the eccentric and mean anomalies

Hence, while we can obtain the mean anomaly (or time) as function of
 , i.e.,
, i.e.,
 , no analytic solutions exist for the reverse problem,
, no analytic solutions exist for the reverse problem,
 . This amounts to solving Kepler's equation — a transcendental equation that must be solved numerically.
. This amounts to solving Kepler's equation — a transcendental equation that must be solved numerically.
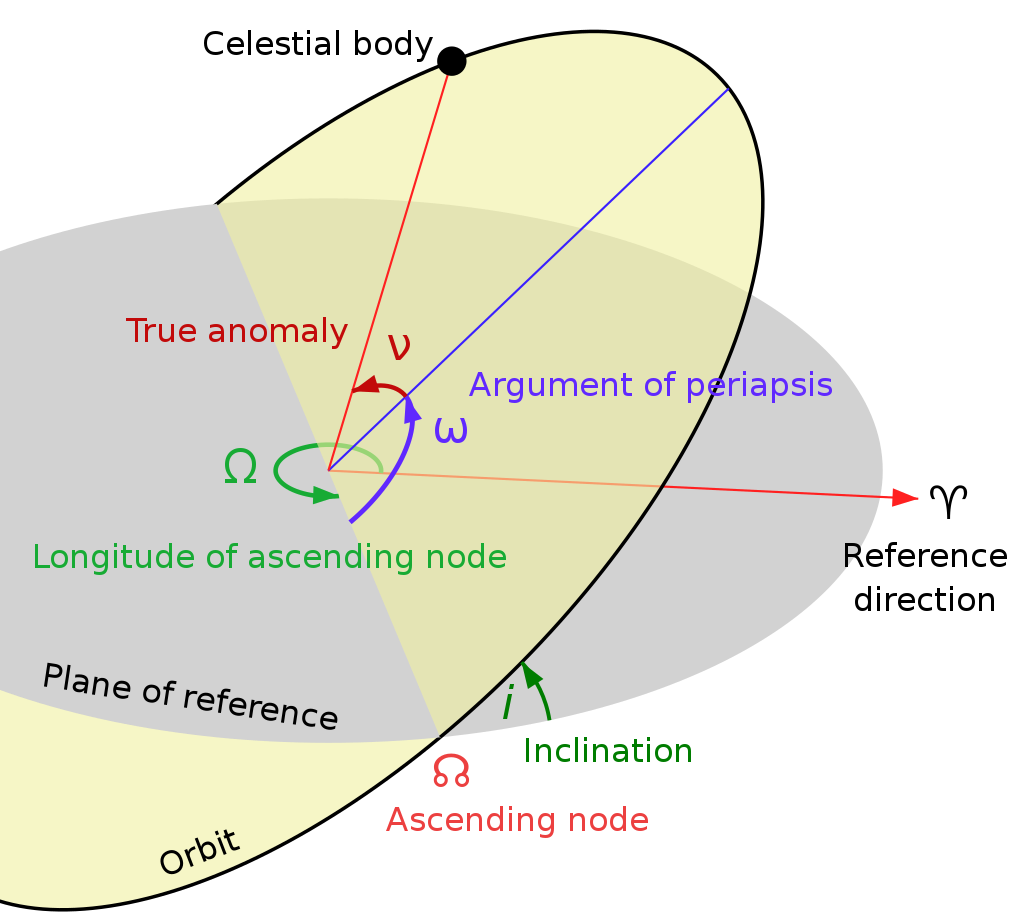
Orbital elements
There are 6 orbital elements:
- semi-major axis a
- eccentricity e
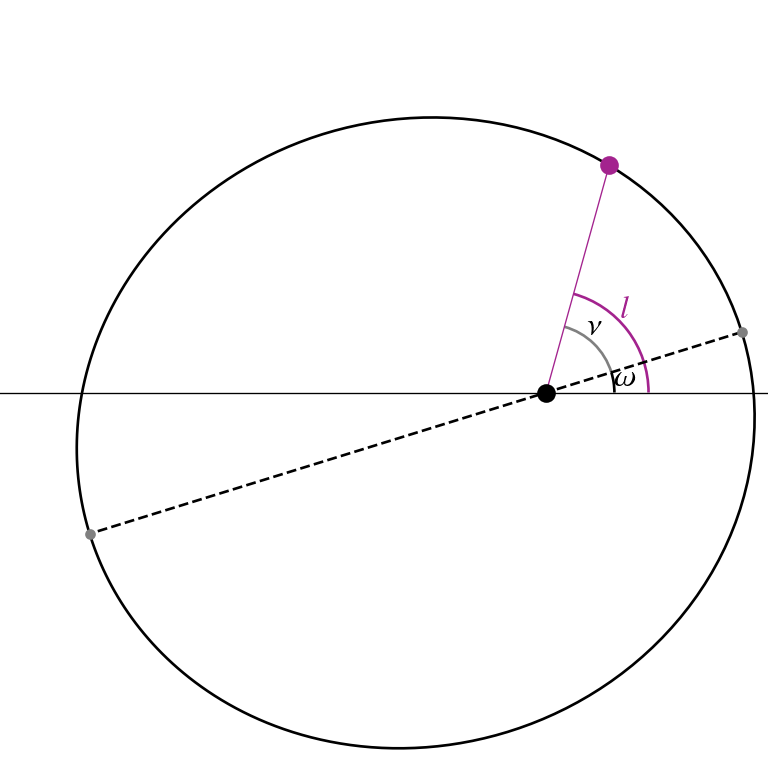
- argument of pericenter ω.
this is the angle with a reference direction. In the planar case the reference is fixed (e.g., the x-axis); in the 3D case, it is the angle with respect to the ascending node Ω.
Sometimes, this angle is replaced by
![]() the longitude of pericenter
the longitude of pericenter
- true anomaly
![]()
the position of the particle w.r.t. pericenter. Equivalently, the true longitude
![]() Another option is to indicate the positon by the mean anomaly M or by the
mean longitude
Another option is to indicate the positon by the mean anomaly M or by the
mean longitude
![]() which is not a geometric angle.
which is not a geometric angle.
for 2D problems, these 4 elements suffice.
Orbital elements
There are 6 orbital elements:
- semi-major axis a
- eccentricity e
- argument of pericenter ω.
- true anomaly
![]()
- inclination i: the angle of the orbit w.r.t. the reference plane.
- longitude of the ascending node (Ω in the figure →). The angle to the line in the reference plane where the particle intersects the reference planet in the ascending direction
Guiding center approximation
In the guiding center approximation the orbit solution, as function of mean anomaly M reads, to first order in eccentricity:

This is a superposition of:
- uniform circular motion (M is linear with time); and
- uniform elliptical motion with the ellipse having a 2:1 aspect ratio.
Note. The 2:1 aspect ratio and the epicycle frequency are valid for a Keplerian potential. This can be generalized to arbitrary potentials.
Note. Historically, pre-Copernican Europeans used circular epicyles to describe the motion of planets under the Ptolemaic model (Earth at center). They did not stop with one epicycle!
↗
Guiding center approximation for a particle in an
 orbit.
orbit.
→
motion with respect to the guiding center.
Circular restricted 3-body problem
read CO 18.1
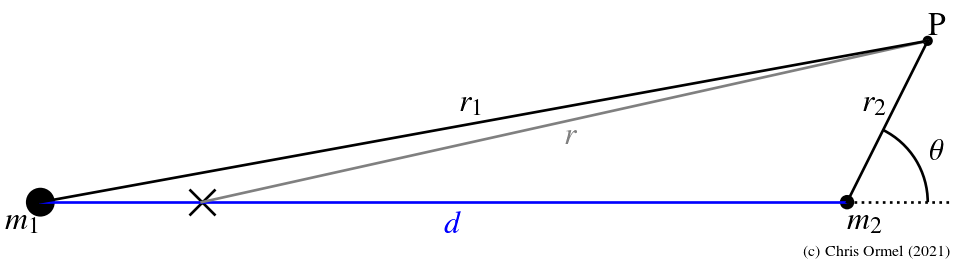
- conduct analysis in comoving, non-inertial frame where bodies 1 and 2 are at rest and:
-
![]() (test particle)
(test particle)
- the binary
![]() is in a circular orbit resulting in the e.o.m.:
is in a circular orbit resulting in the e.o.m.:
![]()
the first term on the RHS is the Coriolis force, the second the centrifugal force. We insert the mean motion of the binary n for ω.
-
- one integral of motion, the
Jacobean energy:
![]()
where
![]() and
and
![]() are the two-body potentials
are the two-body potentials
- The e.o.m. is then
![]()
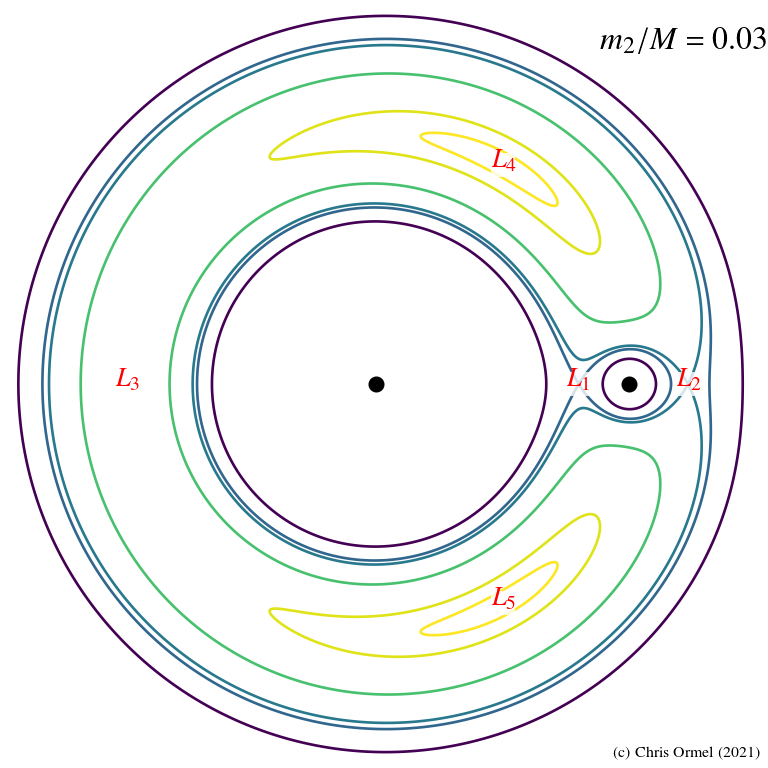
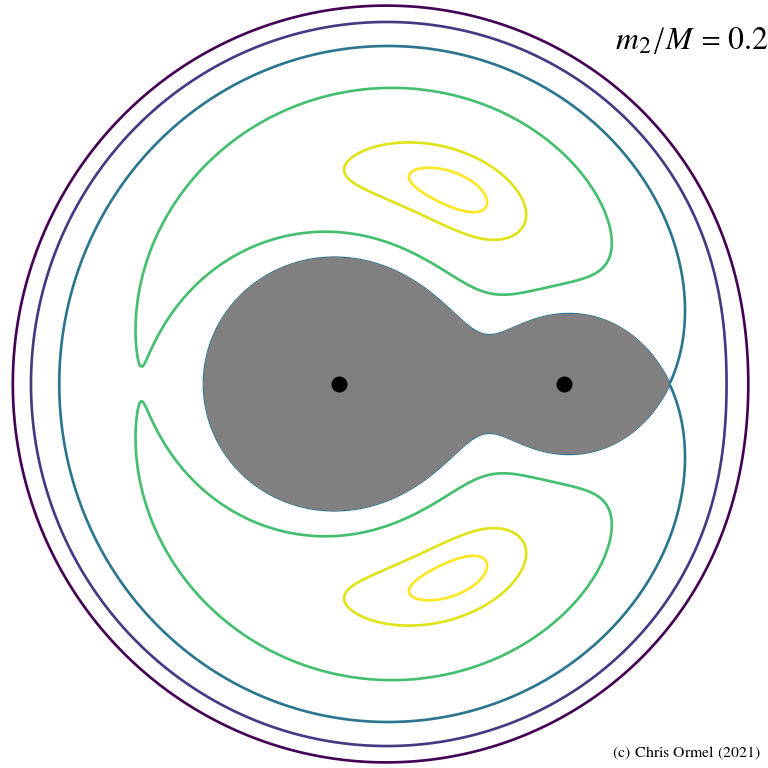
Lagrange points
- Equipotential curves
![]()
in the rotating frame. Applications range from:
— stellar binaries evolution
— dynamics of asteroids - The J value corresponding to these
zero velocity curves
determine the regions that are (potentially) accessible to the particle.
![]()
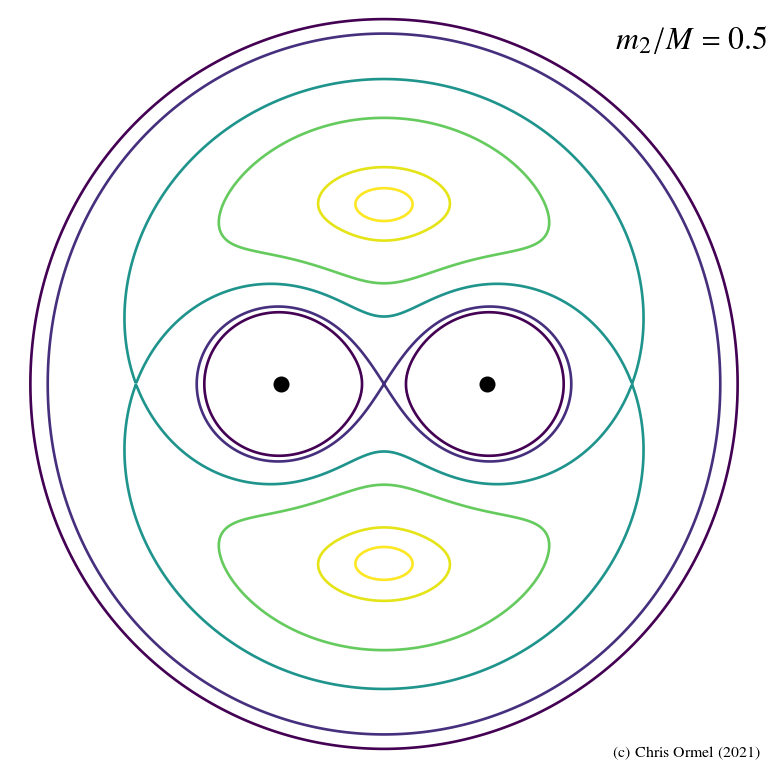
 Lighter contours indicate higher
Lighter contours indicate higher
 darker, lower.
Equal-mass stellar binary.
darker, lower.
Equal-mass stellar binary.
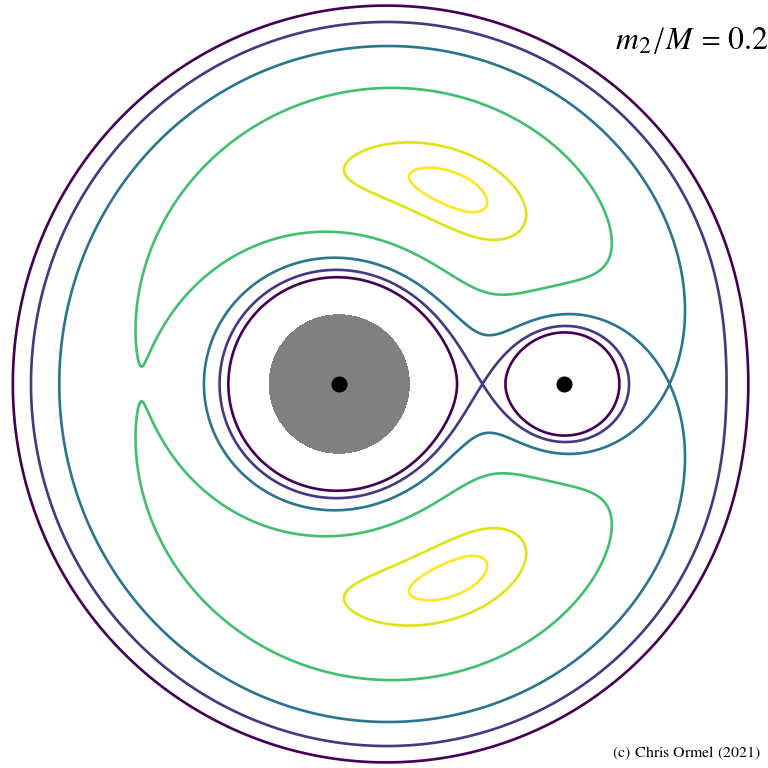
Lagrange points
- Equipotential curves
![]()
in the rotating frame. Applications range from:
— stellar binaries evolution
— dynamics of asteroids - The J value corresponding to these
zero velocity curves
determine the regions that are (potentially) accessible to the particle.
![]()

 Lighter contours indicate higher
Lighter contours indicate higher
 darker, lower.
darker, lower.
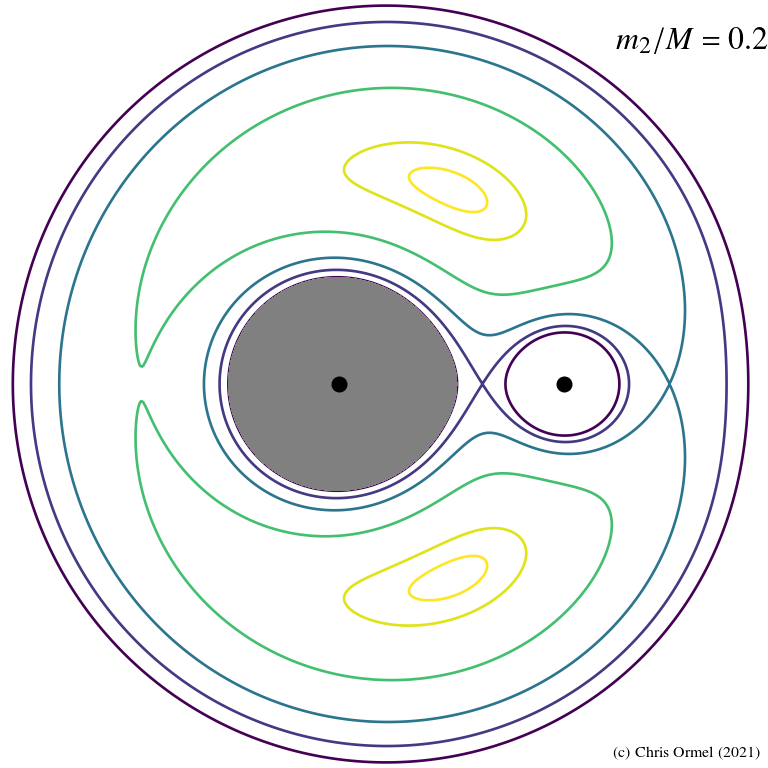
Lagrange points
- Equipotential curves
![]()
in the rotating frame. Applications range from:
— stellar binaries evolution
— dynamics of asteroids - The J value corresponding to these
zero velocity curves
determine the regions that are (potentially) accessible to the particle.
![]()
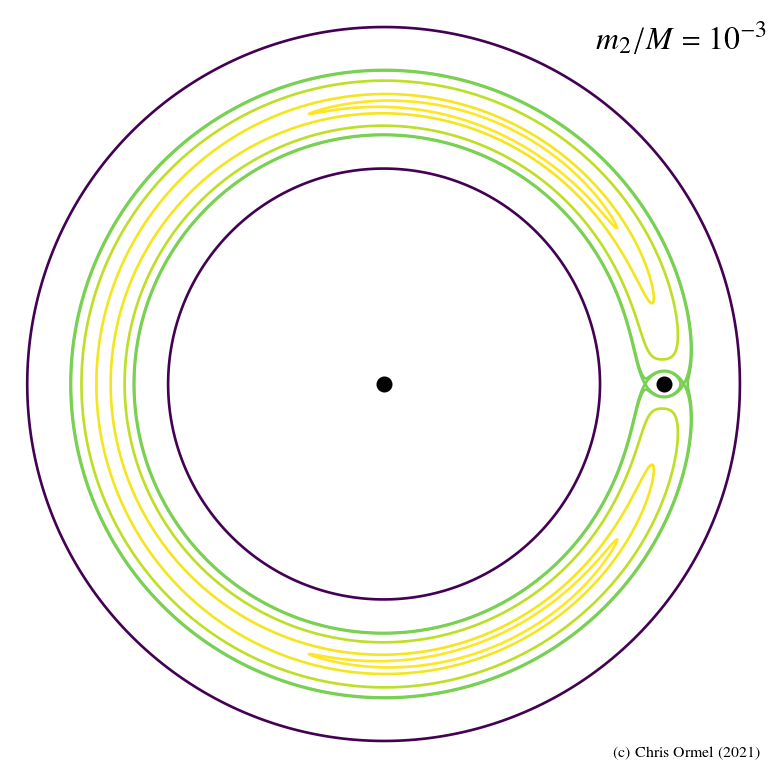
 Lighter contours indicate higher
Lighter contours indicate higher
 darker, lower.
Jupiter/Sun mass ratio.
darker, lower.
Jupiter/Sun mass ratio.
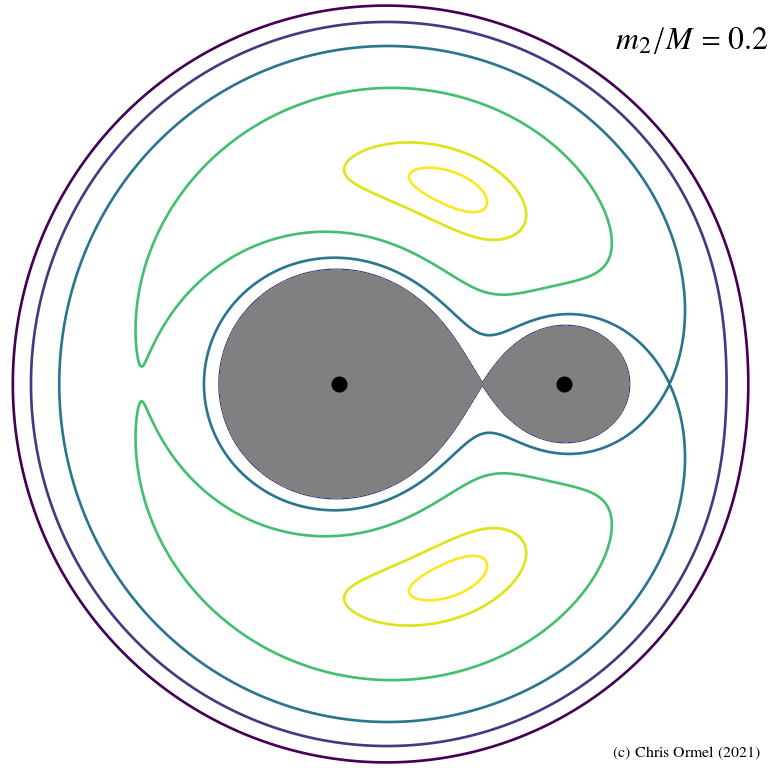
Lagrange points
- Equipotential curves
![]()
in the rotating frame. Applications range from:
— stellar binaries evolution
— dynamics of asteroids - Stationary
Lagrangian points
where the potential vanishes
![]()
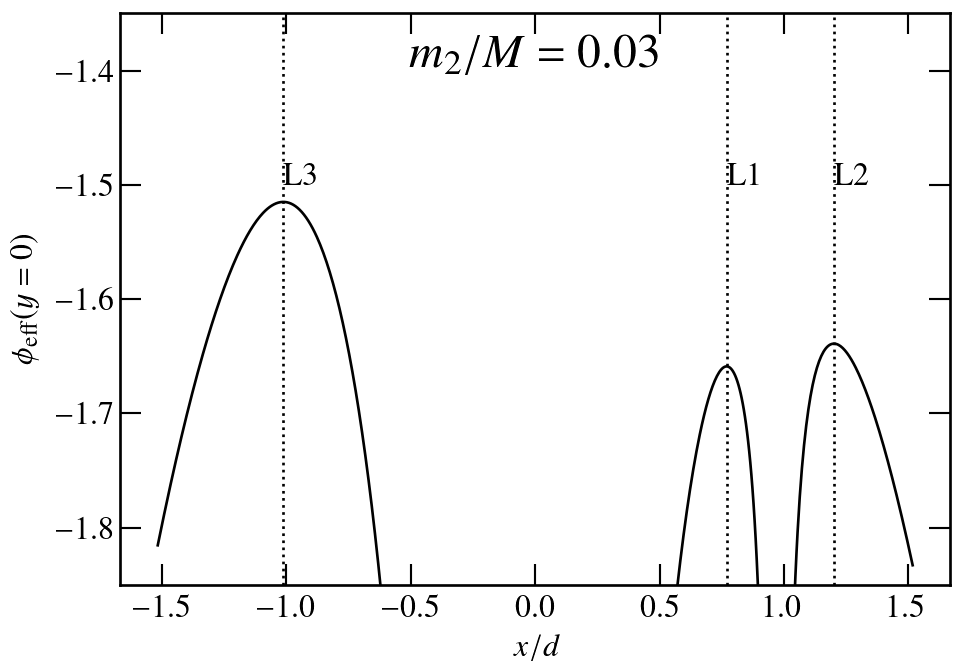
5 in total:
- L1, L2, and L3 along the binary axis, the colinear points
- L4, and L5, the triangular points (r1 = r2 = d)
 Lighter contours indicate higher
Lighter contours indicate higher
 darker, lower.
darker, lower.
Lagrange points
- Equipotential curves
![]()
in the rotating frame. Applications range from:
— stellar binaries evolution
— dynamics of asteroids - Stationary
Lagrangian points
where the potential vanishes
![]()
5 in total:
- L1, L2, and L3 along the binary axis, the colinear points
- L4, and L5, the triangular points (r1 = r2 = d)
- Two types of
coorbital orbits
- Trojans orbit either L4 or L5
- Horseshoes orbit both L4 and L5
Jupiter's Trojans
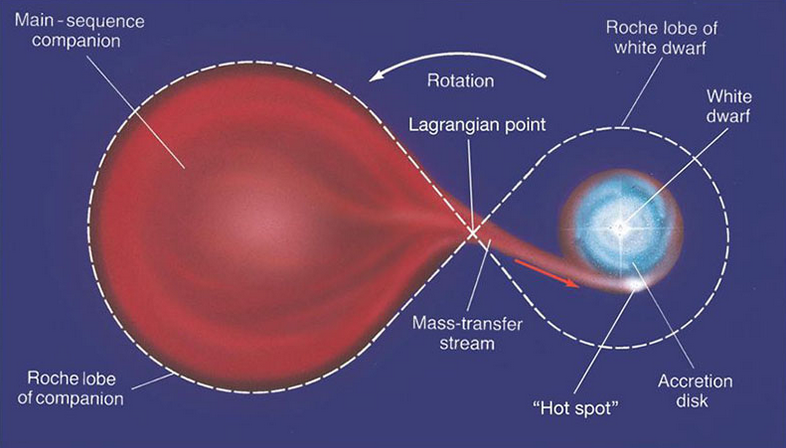
Roche Lobe overflow
Stellar binaries are a classic application of the three-body problem
- One of the stars in the binary expands...
e.g., during the RGB phase. This does not necessarily have to be the most massive star
- The star gradually fill its Roche lobe...
If one star has (almost) fills its Roche lobe, the binary is referred to as semi-detached
- Once it has reached the L1 point, material flows to the secondary
Possible (but not necessarily) it will also fill the Roche Lobe of the secondary.
Accretion onto the secondary can substantially change its evolution - Upon, further expansion, the Roche lobes merge
This is the common envelope phase. The system has now become a contact binary
Roche Lobe overflow
Stellar binaries are a classic application of the three-body problem
- One of the stars in the binary expands...
e.g., during the RGB phase. This does not necessarily have to be the most massive star
- The star gradually fill its Roche lobe...
If one star has (almost) fills its Roche lobe, the binary is referred to as semi-detached
- Once it has reached the L1 point, material flows to the secondary
Possible (but not necessarily) it will also fill the Roche Lobe of the secondary.
Accretion onto the secondary can substantially change its evolution - Upon, further expansion, the Roche lobes merge
This is the common envelope phase. The system has now become a contact binary
Roche Lobe overflow
Stellar binaries are a classic application of the three-body problem
- One of the stars in the binary expands...
e.g., during the RGB phase. This does not necessarily have to be the most massive star
- The star gradually fill its Roche lobe...
If one star has (almost) fills its Roche lobe, the binary is referred to as semi-detached
- Once it has reached the L1 point, material flows to the secondary
Possible (but not necessarily) it will also fill the Roche Lobe of the secondary.
Accretion onto the secondary can substantially change its evolution - Upon, further expansion, the Roche lobes merge
This is the common envelope phase. The system has now become a contact binary
Roche Lobe overflow
Stellar binaries are a classic application of the three-body problem
- One of the stars in the binary expands...
e.g., during the RGB phase. This does not necessarily have to be the most massive star
- The star gradually fill its Roche lobe...
If one star has (almost) fills its Roche lobe, the binary is referred to as semi-detached
- Once it has reached the L1 point, material flows to the secondary
Possible (but not necessarily) it will also fill the Roche Lobe of the secondary.
Accretion onto the secondary can substantially change its evolution - Upon, further expansion, the Roche lobes merge
This is the common envelope phase. The system has now become a contact binary
Roche Lobe overflow
Consequences Roche Lobe overflow
- Accretion. Angular momentum conservation results in an accretion disk
- Energy release. The potential at L1 is much higher than at the surface of the secondary
- Nova
hydrogen spills over and is ignited on the surface of the White Dwarf
- Type 1a supernova
upon reaching the Chandrasekhar mass, the Carbon in the White Dwarf's core will explosively ignite
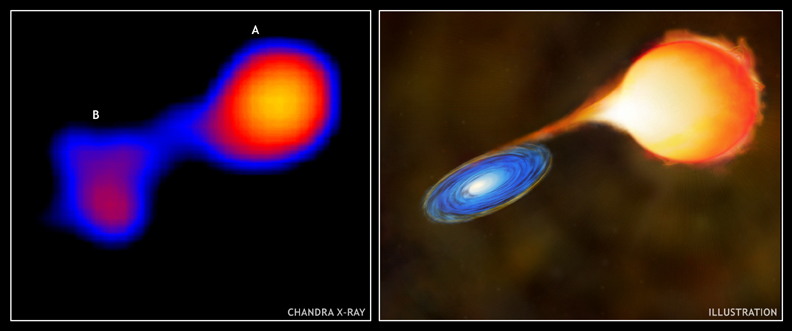
Roche Lobe overflow
Hill's approximation
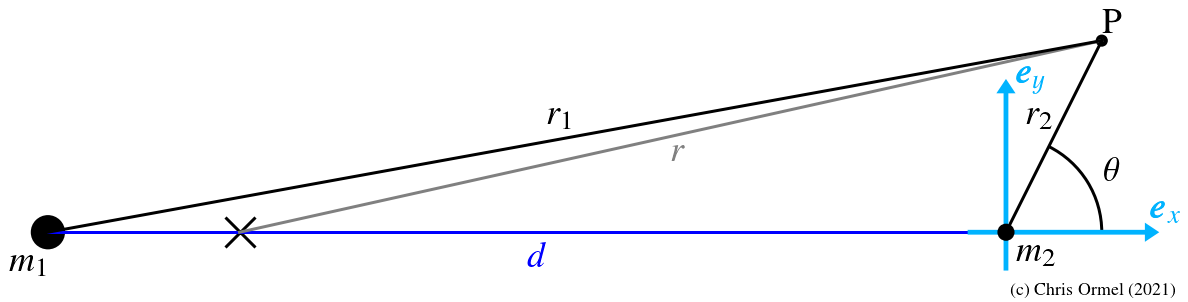
- Expansion of 1/r1 results in
![]()
in the first step, we assumed that r2/d is small; in the second, additionally, that
![]() where
where
![]()
- In Hill's approximation, we put the origin at the secondary;
Hill's approximation

- In Hill's approximation, we put the origin at the secondary;
- The L1 and L2 points lie at a distance
which is known as the Hill radius.
![]()
Interpretation. At distances
![]() we can ignore m1's (the stellar) gravity; at distances
we can ignore m1's (the stellar) gravity; at distances
![]() the secondary's gravity amounts to a small perturbation (small angle scattering). At distances
the secondary's gravity amounts to a small perturbation (small angle scattering). At distances
![]() both bodies contribute equally, giving rise to complex 3-body dynamics.
both bodies contribute equally, giving rise to complex 3-body dynamics.
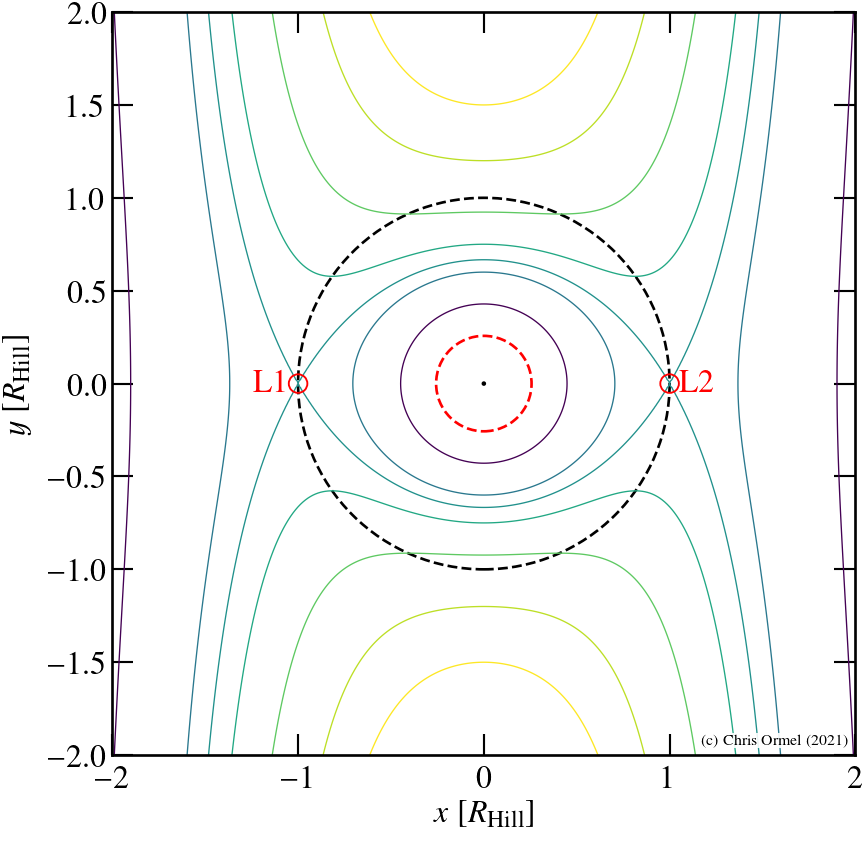
 in the Hill approximation (these are not orbits!). As
in the Hill approximation (these are not orbits!). As
 has become symmetric with respect to x=0, so are L1 and L2. Coordinates are normalized with respect to
has become symmetric with respect to x=0, so are L1 and L2. Coordinates are normalized with respect to
 In these units, Earth radius would be 0.00425 (black dot and the center) and the Moon orbits at r=0.2569 (dashed red circle).
In these units, Earth radius would be 0.00425 (black dot and the center) and the Moon orbits at r=0.2569 (dashed red circle).
Hill's approximation
- The L1 and L2 points lie at a distance
which is known as the Hill radius.
![]()
Interpretation. At distances
![]() we can ignore m1's (the stellar) gravity; at distances
we can ignore m1's (the stellar) gravity; at distances
![]() the secondary's gravity amounts to a small perturbation (small angle scattering). At distances
the secondary's gravity amounts to a small perturbation (small angle scattering). At distances
![]() both bodies contribute equally, giving rise to complex 3-body dynamics.
both bodies contribute equally, giving rise to complex 3-body dynamics.
- The e.o.m. are, in terms of Cartesian coordinates x, y :
![]()
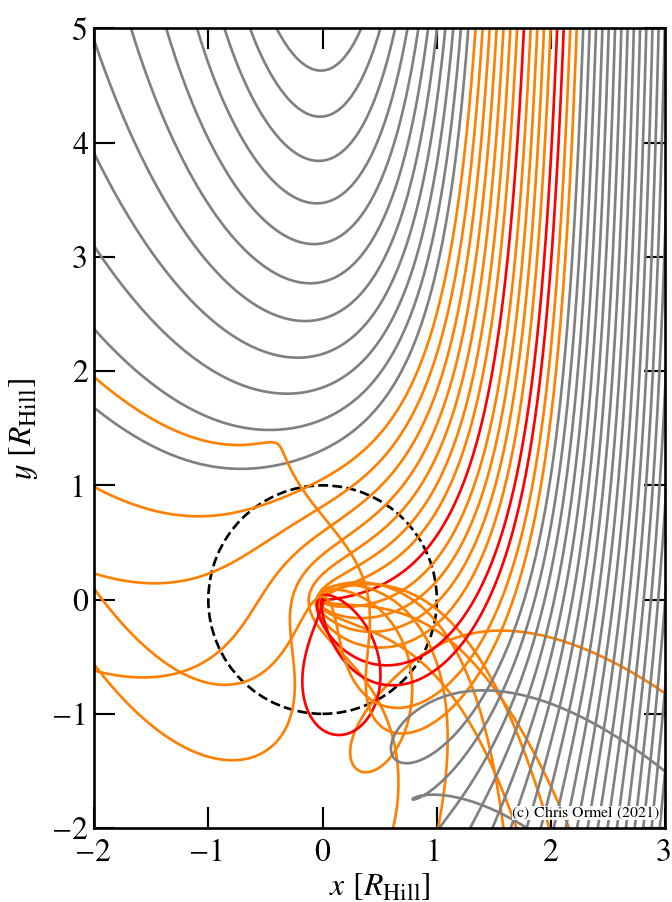
→ sample integrations of trajectories in Hill's approximation. Particles initially have 0 eccentricity. Grey: particles do not enter the Hill sphere; orange: particles enter and exit the Hill sphere; red: particles that accrete onto the planet Encounters that enter the Hill sphere will experience strong scatterings.
Roche limit
read CO 19.2
- The
Roche limit
refers to the point where the secondary overflow its Roche lobe; it is tidally destructed when
![]() or at a distance
or at a distance
![]()
Based on the Hill radius expression, the prefactor should have been 31/3. But the point-mass assumptions underlying these expressions are no longer be valid at the point where bodies are tidally torn apart. The expression (first derived by Eduard Roche) accounted for these effects
Note in case of planet satellites, we are represented with a hierarchy: star—planet—satellite. We say that the satellite orbits within the planet's Hill sphere, and that they are destroyed once they pertrude inside the planet's Roche limit.
- Therefore, each body has:
- a Roche limit, determined by the density ratio with a (smaller) secondary body
- a Hill sphere, determined by the mass ratio and the distance to a larger (primary) body

Roche limit
Tides
read CO 19.2
- Evaluate the effective potential at
![]() :
:
![]()
where
![]() is the tidal potential and
is the tidal potential and
![]() is the Legendre polynomial.
is the Legendre polynomial.
- The tidal acceleration on the planet's surface is
![]()
where the components are the Cartesian x and y. Tides on a planet are created due to a difference in the gravitational force of the perturber over its surface.
- The (half-) amplitude of the
tidal bulge
is estimated as
![]()
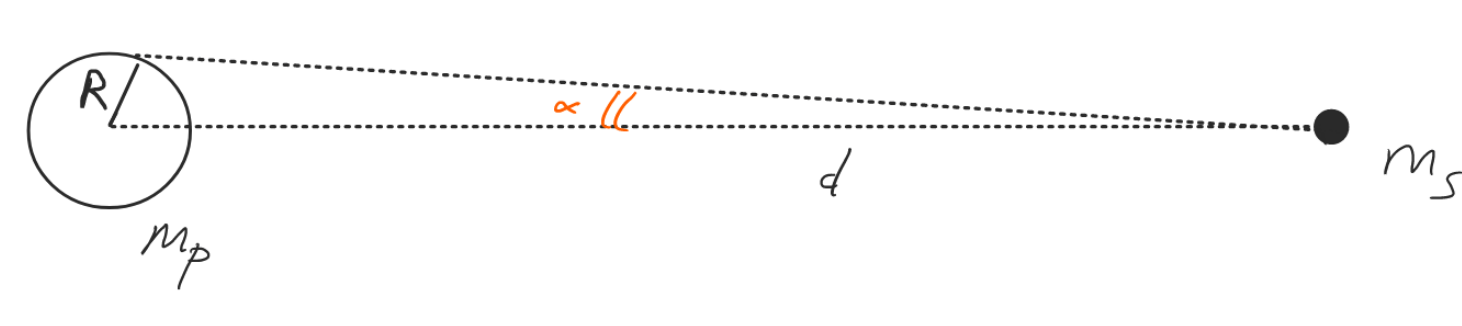
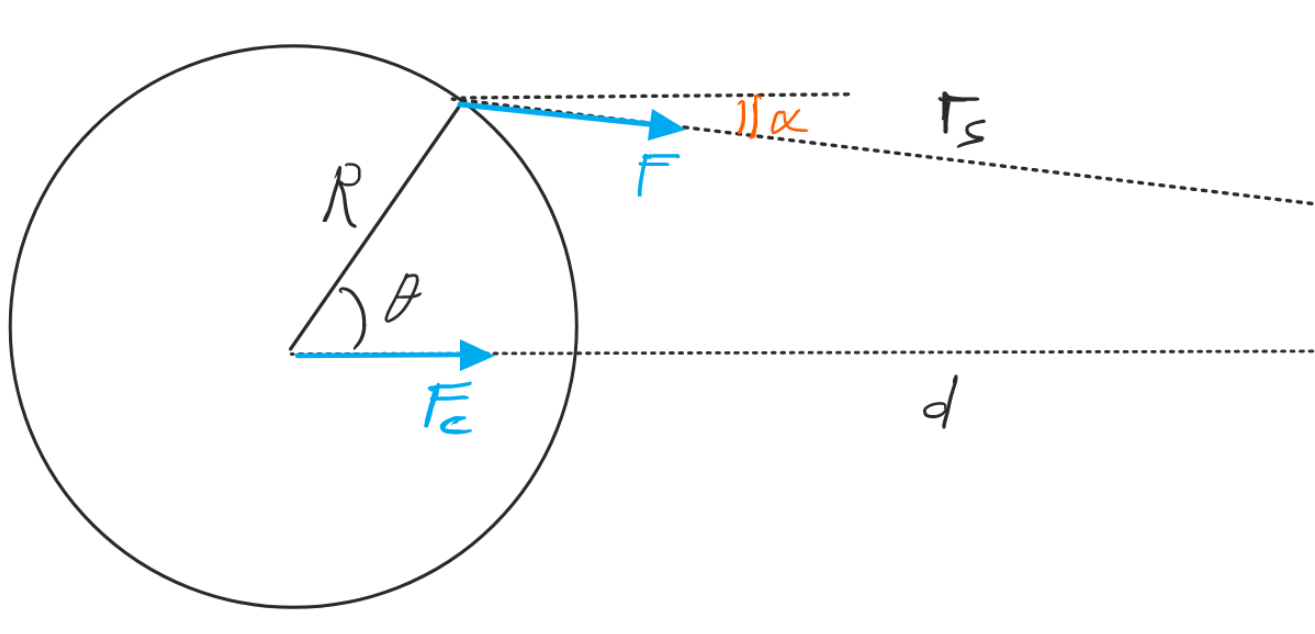
Q: What are the amplitudes of the tides on the Earth, induced by the Moon and the Sun, respectively?
Tides
read CO 19.2
- Evaluate the effective potential at
![]() :
:
![]()
where
![]() is the tidal potential and
is the tidal potential and
![]() is the Legendre polynomial.
is the Legendre polynomial.
- The tidal acceleration on the planet's surface is
![]()
where the components are the Cartesian x and y. Tides on a planet are created due to a difference in the gravitational force of the perturber over its surface.
- The (half-) amplitude of the
tidal bulge
is estimated as
![]()
for the Earth this gives a tide (full amplitude) of 71cm (Moon) and 33cm (Sun)?
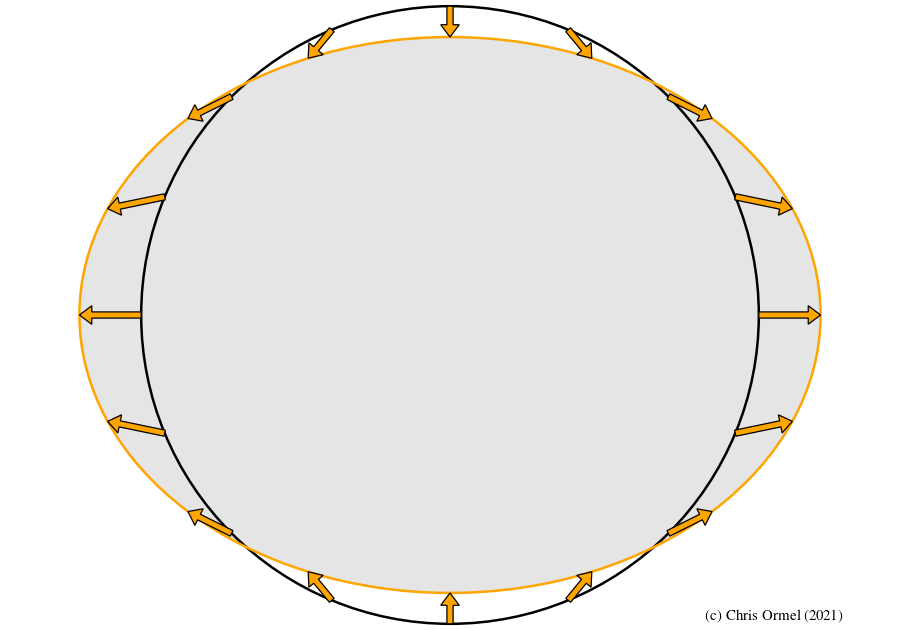
tidal torque & energy dissipation
- Due to friction, the tidal bulge is mis-aligned with the planet by an angle
![]() the
lag angle
the
lag angle
- The
tidal quality factor Q
expresses the rate at which the energy contained in the tidal bulge dissipates
It's defined as
![]()
where
![]() is the tidal frequency — for a diurnal tide (Earth-Moon system)
is the tidal frequency — for a diurnal tide (Earth-Moon system)
![]() — and
— and
![]() is the maximum energy stored in the tidal deformation.
This expression arises, because it is reasonable to expect that the rate of energy dissipation
is the maximum energy stored in the tidal deformation.
This expression arises, because it is reasonable to expect that the rate of energy dissipation
![]() is proportional to tidal frequency and
is proportional to tidal frequency and
![]() .
.
- If there is time delay
![]() between the tidal forcing and the tidal response, it is straightforward to show that
between the tidal forcing and the tidal response, it is straightforward to show that
![]() .
.
- In the case of an diurnal tide, a lag of
![]() between forcing & response corresponds to an angle of
between forcing & response corresponds to an angle of
![]() . Hence,
. Hence,
![]() .
.
- If there is time delay
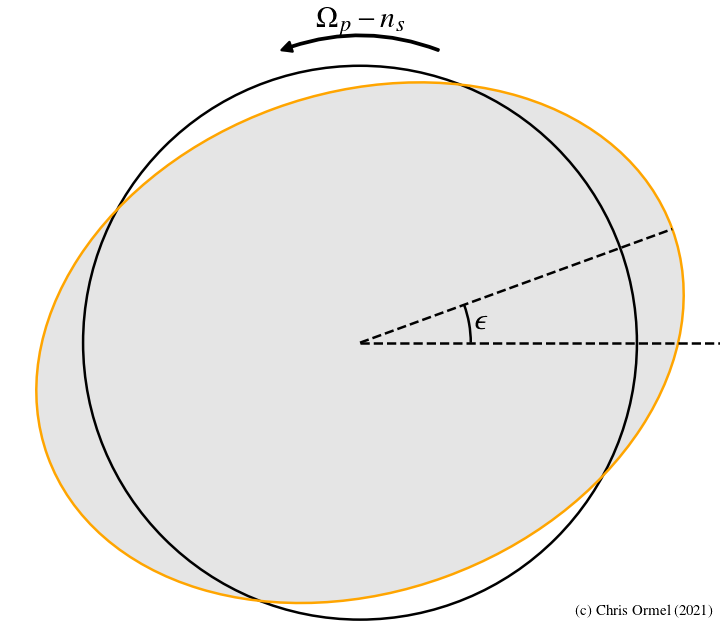
 . When the planet spin frequency exceeds the mean motion of the secondary,
. When the planet spin frequency exceeds the mean motion of the secondary,
 the tidal bulge is pulled ahead (positive ε). In this siutation, maximum tide occur after the conjunction.
the tidal bulge is pulled ahead (positive ε). In this siutation, maximum tide occur after the conjunction.
tidal torque & energy dissipation
- Due to friction, the tidal bulge is mis-aligned with the planet by an angle
![]() the
lag angle
the
lag angle
- The tidal quality factor Q expresses the rate at which the energy contained in the tidal bulge dissipates
- The (tilted!) tidal bulge results in a back-reaction force on the planet, which:
- dissipates energy at rate
![]() :
:
This heats the planets (tidal heating) at the expense of the total spin and orbital angular momentum
- produce a torque
![]() on the satellite
on the satellite
- For positive ε (a tidal lag), Γ is positive, the satellite gains orbital angular momentum, whereas the planet spins down. Angular momentum is transferred from the planet (spin) to the satellite (orbit) .
- Vice-versa for negative ε. As a result the system will move towards
co-rotation
where the orbit's mean motion equals the spin rotation rate:
![]()

| planet | quality factor | Love number | inertia factor |
|---|---|---|---|
| Q | k2 | CI | |
| Earth | 12 | 0.3 | 0.33 |
| Moon | 12 | 0.3 | 0.33 |
| Mars | (100) | 0.14 | 0.364 |
| Io | (100) | 0.03 | 0.364 |
| planet internal data | |||
Tidal torque
- The tidal bulge generates a quadrupole potential
![]()
This can be understood as follows. The excess/deficit mass in the tidal bulge is
![]() . The quadrupole potential generated by
. The quadrupole potential generated by
![]() will be be proportial to
will be be proportial to
![]() ,
,
![]() and
and
![]() where
where
![]() is aligned with the bulge. Finally,
k2p — the
Love number
— encapsulates all our uncertainty regarding the tidal response. For example, rigid planets will have small
is aligned with the bulge. Finally,
k2p — the
Love number
— encapsulates all our uncertainty regarding the tidal response. For example, rigid planets will have small
![]() .
.
In expressions like these, the tidal lag parameter ε is usually replaced by the tidal quality factor Qp.
- The net energy (loss) is
![]() .
.
(for positive ΓT) the satellite gains energy while the planet loses energy
Q: What happens to this energy?

↑
In a reference frame aligned with the tidal bulge, the quadrupole potential it generates
is
 with
with
 the positive x-axis. In this frame the satellite is located at
the positive x-axis. In this frame the satellite is located at
 (in case of a tidal lag). The tidal torque on the satellite is:
(in case of a tidal lag). The tidal torque on the satellite is:

The torque is defined positive for satellites beyond the synchronization radius (positive lag angle and increase in orbital energy). Otherwise, Γ is negative.
Tidal torque
- The tidal torque elevates the orbit of the satellite while spinning down the planet
![]()
where
![]() is the moment of inertia of the planet
is the moment of inertia of the planet
![]() its spin, mμ the reduced mass,
its spin, mμ the reduced mass,
![]() the mean motion
and
the mean motion
and
![]() the semi-major axes of the orbit.
the semi-major axes of the orbit.
- Energy is dissipated in the planetary body
![]()
- Key timescales
![]()
where
![]() is the moment of inertia of the planet and signs are consistent with a positive torque (orbit expands and planet spins down).
is the moment of inertia of the planet and signs are consistent with a positive torque (orbit expands and planet spins down).

Role of Planet and Satellite can be interchanged
-
Due to symmetry considerations, these expressions can also be used to calculate tides planets induce on satellites simply by
interchanging indices:
![]() (!)
(!)
- Expressions also apply when the "satellite" is much more massive, for example as in the Earth-Sun system (with the far more massive Sun in the role of the satellite!)
Eccentricity tides
The equations

also hold when there is no (net) torque (
 )!
)!
Note.: In discussion below
(↓),
and
(↗)
I have interchanged the satellite/planet (
 ) as it is more usual that a massive body (planet/star) induces tides in a smaller body (satellite/planet).
) as it is more usual that a massive body (planet/star) induces tides in a smaller body (satellite/planet).
When the satellite is
tidally locked
(
 ), there is no (fixed/net) tidal lag:
), there is no (fixed/net) tidal lag:
 and
and
 does not change. However, tides still operate, e.g., when the satellite is inclined or is in an eccentric orbit. This is because tides dissipate energy in the interior of the planet (
does not change. However, tides still operate, e.g., when the satellite is inclined or is in an eccentric orbit. This is because tides dissipate energy in the interior of the planet (
 ), resulting in energy being extracted from the orbit and circularizing it (due to angular momentum conservation).
), resulting in energy being extracted from the orbit and circularizing it (due to angular momentum conservation).
↑ Tidal forcing due to a satellite on an eccentric orbit, in a frame where the guiding center (open circle) is at rest. As the planet is tidally locked, there is no rotation in this frame (black arrow is fixed). The tidal bulge follows (but lags) the position of the satellite. Energy is dissipated due to the radial and azimuthal flexing of the bulge. The tidal deformation and lag angle are greatly exaggerated for illustrative purposes.
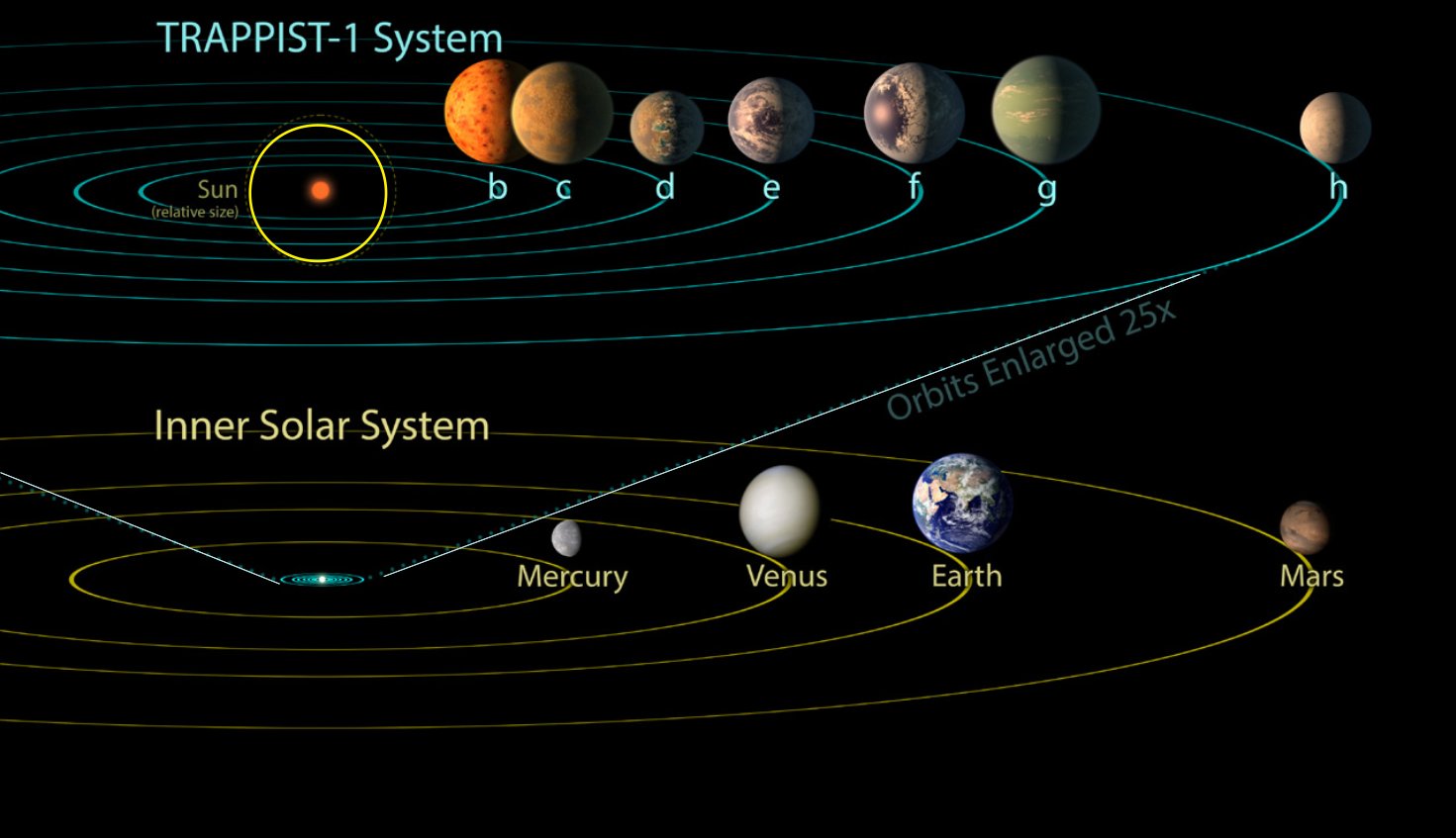
Application: Trappist-I system
Are the TRAPPIST-1 planets tidally locked?

where tides are due to the 0.09 solar-mass star. For d and n I have inserted values for the outer-most planets.
It is therefore very likely that all its planets are tidally locked!
Since the system age is many Gyr old
Io
- what powers its volcanoes?
- why no craters?
Orbital resonances
The Galilean satellite system is an example of three-body resonance (Laplace resonance)
The period ratios of the planets obey a conmensurability, where the orbital period ratio is a rational number:

- same for the second and third planet
- o is called the resonance order
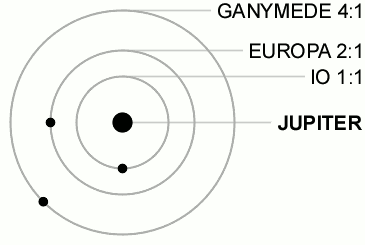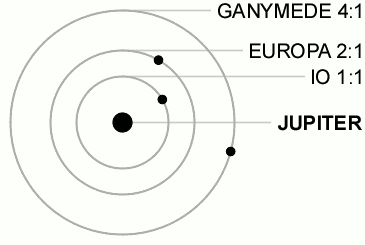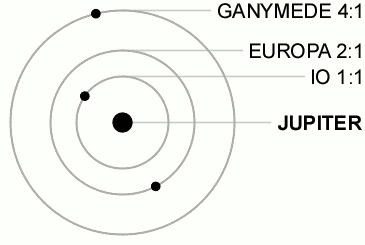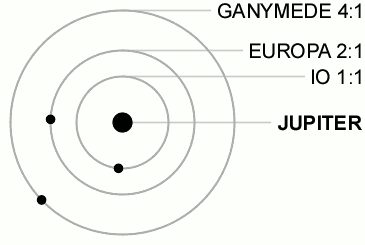
resonance or not?
Q: Shown are planets at/near a 3:2 mean motion resonance. Inner body is on a circular orbit, outer on an eccentric. Which are in resonance?
resonance or not?
Resonances
- Consider a first order j:j+1 resonance between
- an inner planet on a circular orbit
- an exterior planet on an eccentric orbit
- Let the
resonance angle
be defined
![]()
Hence, the resonance angle corresponds to the mean anomaly M2 at conjuction. When
![]() is fixed, conjunction always take place at the same point in the orbit.
is fixed, conjunction always take place at the same point in the orbit.
- Generally, the condition for resonance is that
![]() librates
around a fixed value
librates
around a fixed value
That is,
![]() is restricted to a certain range.
To librate contrasts to circulate — in that case
is restricted to a certain range.
To librate contrasts to circulate — in that case
![]() takes on all values
between 0 and 360 degrees.
takes on all values
between 0 and 360 degrees.
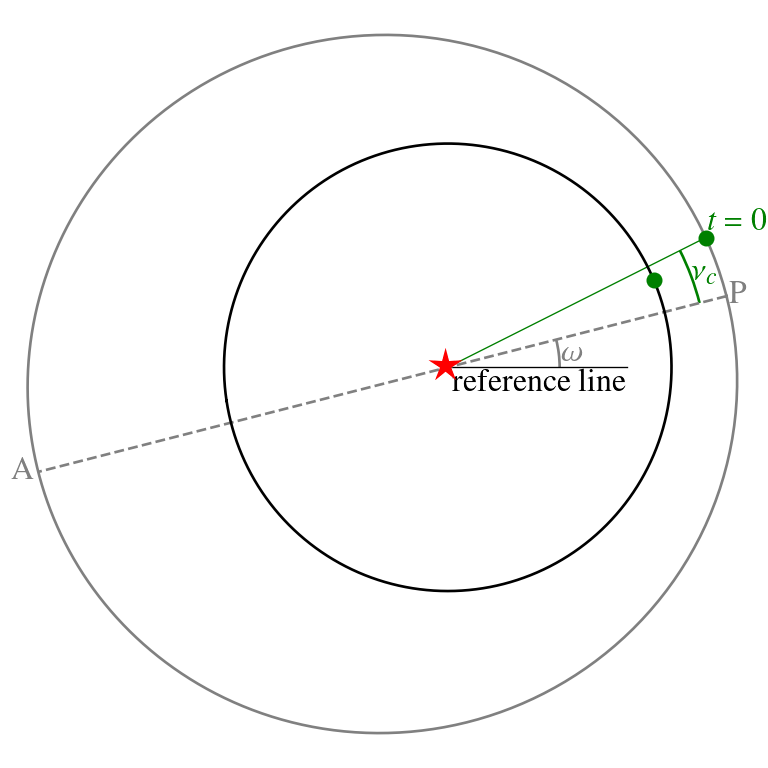
physics of resonances
- At conjunction, the inner planet 1 overtakes the outer planet 2
- a net gain in angular momentum
- a net loss
- no change
- closer to pericenter
- further from pericenter
- no change
→ inner planet on circular orbit; outer on eccentric orbit with conjunctions just past pericenter. Positions at equal times are connected by dots.
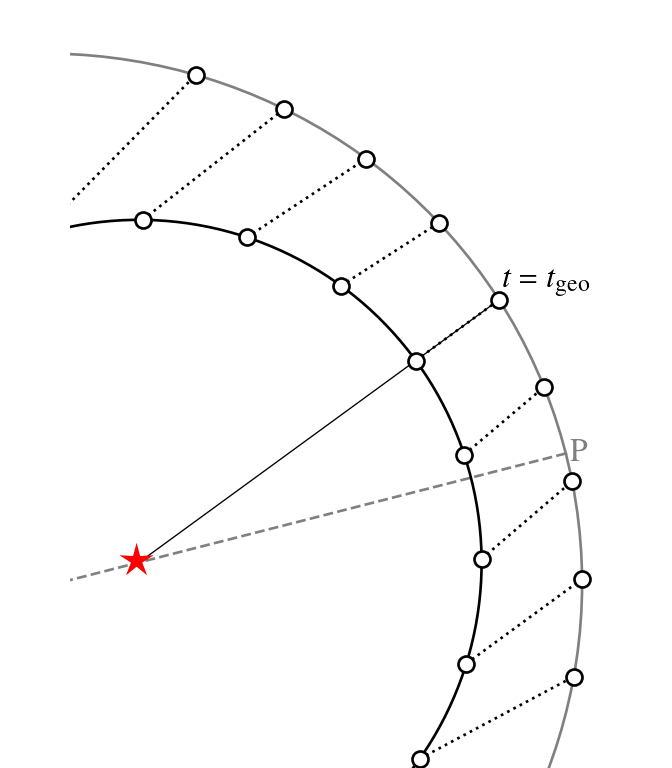
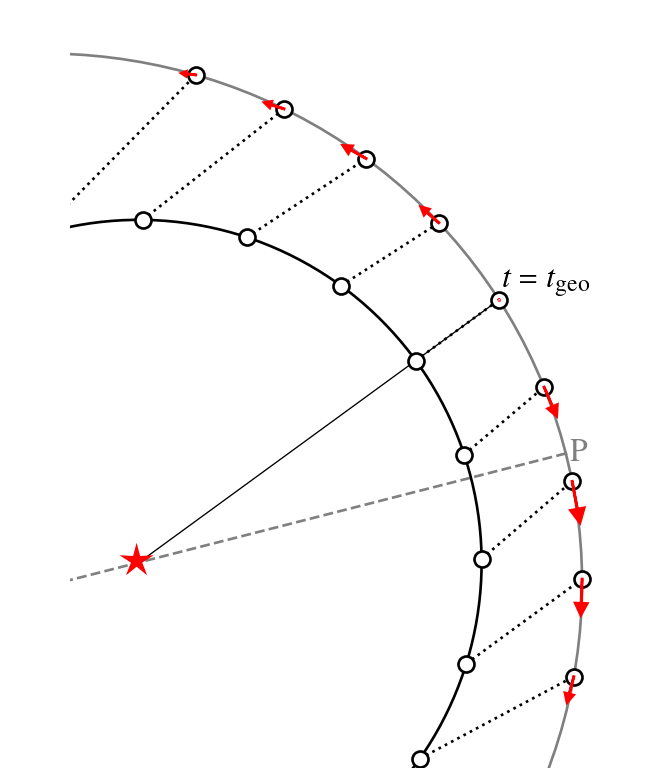
physics of resonances
- At conjunction, the inner planet 1 overtakes the outer planet 2
for an eccentric outer planet, stable conjunctions take place at apocenter.
- If the conjuction is not precisely at pericenter (apocenter) the encounter is asymmetric:
- the distance pre- and post encounter;
- the relative motion pre- and post encounter;
- The asymmetry results in a net torque on planet 2, which changes its angular momentum
![]()
where Fθ is the azimuthal component and Δl the change in angular momentum of planet 2.
→ inner planet on circular orbit; outer on eccentric orbit with conjunctions just past pericenter. Positions at equal times are connected by dots. Before the conjunction 2 experiences a gravitational force (from 1) opposite to its direction of motion. After the encounter, planet 1 pulls planet 2 along. Only the azimuthal component of the direct force is shown with red arrows. In this setup the resonance would move to apocenter.
resonance trapping
The resonance forcing equations for a first order (j+1:j) resonance read:

 ,
,
 is the mean motion of the inner perturber and (
is the mean motion of the inner perturber and (
 ) refer to the outer body on an eccentric orbit.
) refer to the outer body on an eccentric orbit.
Notes:
- For the perturber on an outer, circular orbit, re-label 1→2. Furthermore,
![]() and
and
![]() . See Table for values of
. See Table for values of
![]() .
.
- Expressions are valid to first order in eccentricity only.
-
![]() has been substituted for ω through the resonance angle
and
has been substituted for ω through the resonance angle
and
![]() has been defined as a "distance" from resonance.
has been defined as a "distance" from resonance.
- These expression only hold water if
![]() librates (domain of
librates (domain of
![]() is restricted).
is restricted).
- If
![]() does not librate, there is no resonance forcing.
But, to second order in eccentricity (expressions proportional to e2), eccentricity can still be forced in the non-resonant (secular) way.
does not librate, there is no resonance forcing.
But, to second order in eccentricity (expressions proportional to e2), eccentricity can still be forced in the non-resonant (secular) way.
| j | Gje (inner) | Gje (outer) |
|---|---|---|
| 1 | -0.214 | 1.50 |
| 2 | -1.66 | 2.32 |
| 3 | -2.46 | 3.13 |
| 4 | -3.27 | 3.93 |
| 5 | -4.07 | 4.73 |
| 6 | -4.87 | 5.54 |
valid for an inner perturber on a circular orbit (left column; with δ1=1) or an outer perturber on circular orbit (right column; with δ2=0)
resonance trapping
Several applications and insights follow from these equations
- the timescale over which
![]() oscillates — the
libration time
— and the
libration width
oscillates — the
libration time
— and the
libration width
- the condition for trapping into resonance.
Another, complementary way to study these problems are direct N-body integrations, which numerically solve the equation of motion.
initialize_resonances.py ipython notebook script.
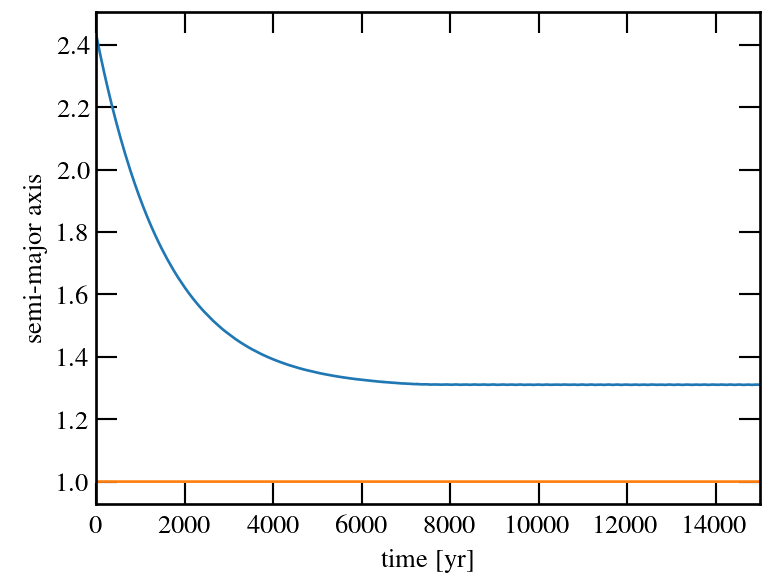
resonance trapping
Several applications and insights follow from these equations
- the timescale over which
![]() oscillates — the
libration time
— and the
libration width
oscillates — the
libration time
— and the
libration width
- the condition for trapping into resonance.
Another, complementary way to study these problems are direct N-body integrations, which numerically solve the equation of motion.
initialize_resonances.py ipython notebook script.

resonance trapping
Several applications and insights follow from these equations
- the timescale over which
![]() oscillates — the
libration time
— and the
libration width
oscillates — the
libration time
— and the
libration width
- the condition for trapping into resonance.
Another, complementary way to study these problems are direct N-body integrations, which numerically solve the equation of motion.
initialize_resonances.py ipython notebook script.
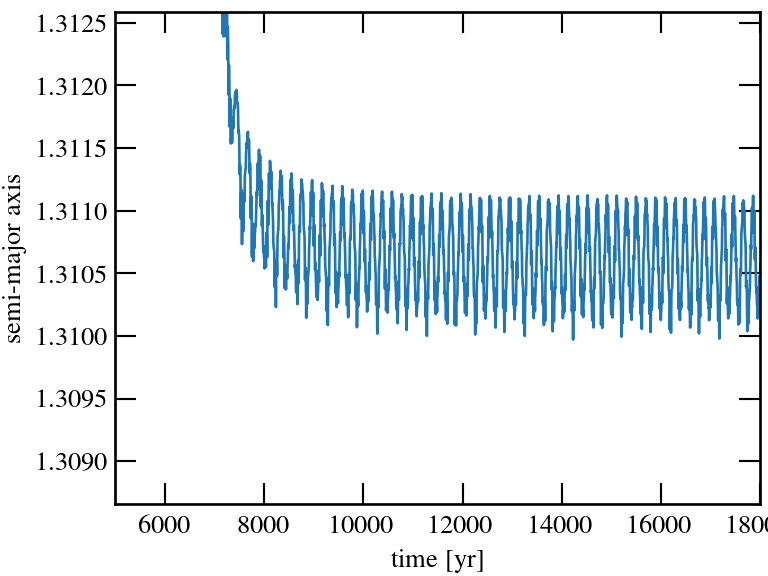
width
exoplanet resonances
Do planets get trapped?
- certain systems, like TRAPPIST-1, are characterized by a many-planet resonance chain
in case of TRAPPIST-1, its seven planets are located near 8:5, 5:3, 3:2, 3:2, 4:3, and 3:2.
- statistically, there is an excess of the planet frequency at resonance locations
certainly not every planet pair is now in resonance, e.g., solar system
exoplanet resonances
Do planets get trapped?
- certain systems, like TRAPPIST-1, are characterized by a many-planet resonance chain
in case of TRAPPIST-1, its seven planets are located near 8:5, 5:3, 3:2, 3:2, 4:3, and 3:2.
- statistically, there is an excess of the planet frequency at resonance locations
certainly not every planet pair is now in resonance, e.g., solar system

end of module 7
—congrats—